SQL 也能递归?一文搞懂 Recursive CTE的魔力
很多人以为递归(Recursive)只属于编程语言,和 SQL 没什么关系。但其实 SQL 中也能实现递归操作,特别是在处理树结构、路径查找时,WITH RECURSIVE 展现出强大威力。本文将带你一步步掌握 SQL 中的递归查询,揭开 Recursive CTE 的神秘面纱!
Recursive CTE(递归公共表表达式)
在 SQL 中,递归公共表表达式(Recursive CTE) 是一种强大的查询手段。通过 WITH RECURSIVE 语法,开发者可以定义一个可以引用自身的查询结构,实现在查询过程中“自我迭代”的效果。
简单来说,SQL 也能“递归”。
不过需要注意的是,递归查询必须设计得当,确保它在某个条件下能够终止。否则,就可能陷入“无限循环”,导致查询无法完成,甚至拖垮数据库性能。
那么,SQL 的递归到底怎么写?能解决哪些实际问题?接下来,我们就从原理、写法,到典型应用场景,一步步带你搞懂 Recursive CTE 的魔力。
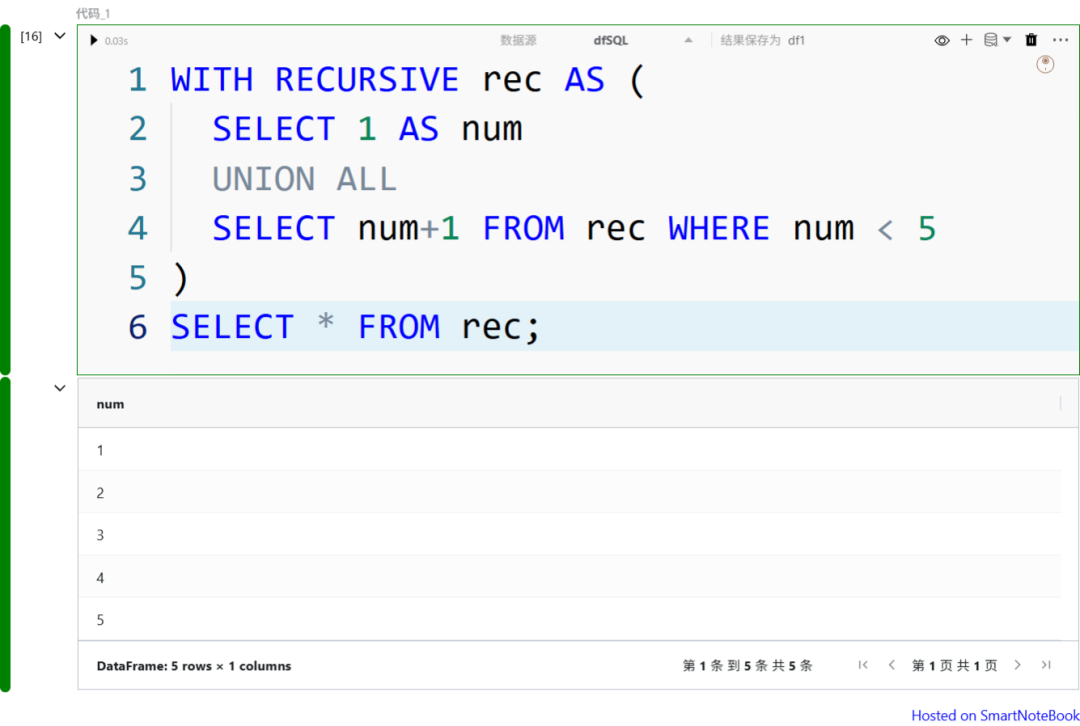
来看一个最简单的例子,生成从 1 到 5 的数字序列:
 图片
图片
我们来拆解一下这段 SQL 是如何“递归”的:
- 首先,SELECT 1 AS num 是 递归的起点,称为锚点(Anchor Member),递归从这里开始。
- 接下来,SELECT num + 1 FROM rec WHERE num < 5 是 递归部分,它会反复执行,直到 num < 5 不再满足为止。
- UNION ALL 将锚点和递归部分的结果组合起来。
整个查询的执行过程大致如下:
- 第一步,输出 1;
- 然后执行递归部分,1 + 1 = 2,满足条件,继续;
- 依次得到 3、4、5;
- 当 num 增加到 6 时,不满足 num < 5,递归终止。
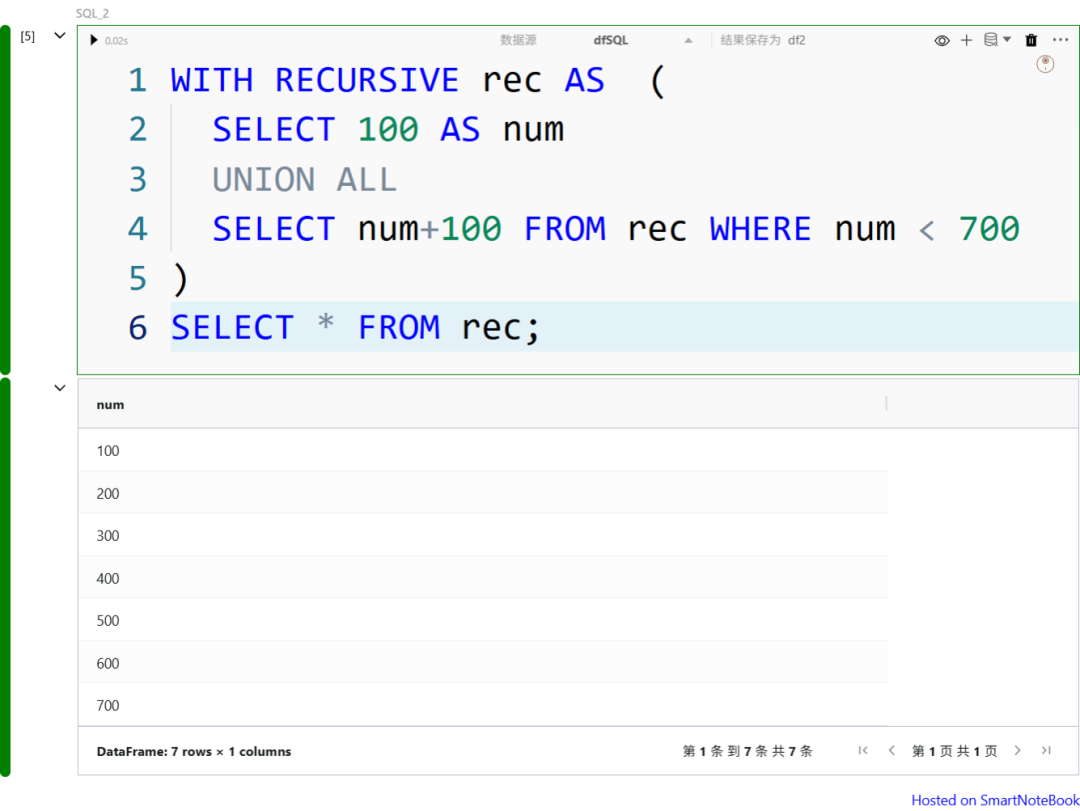
把递归逻辑“套”起来,这次不是 1 到 5,而是 100、200、300……直到 700。核心逻辑没变,只是换了组数字而已。
 图片
图片
示例:斐波那契数列(Fibonacci Sequence)
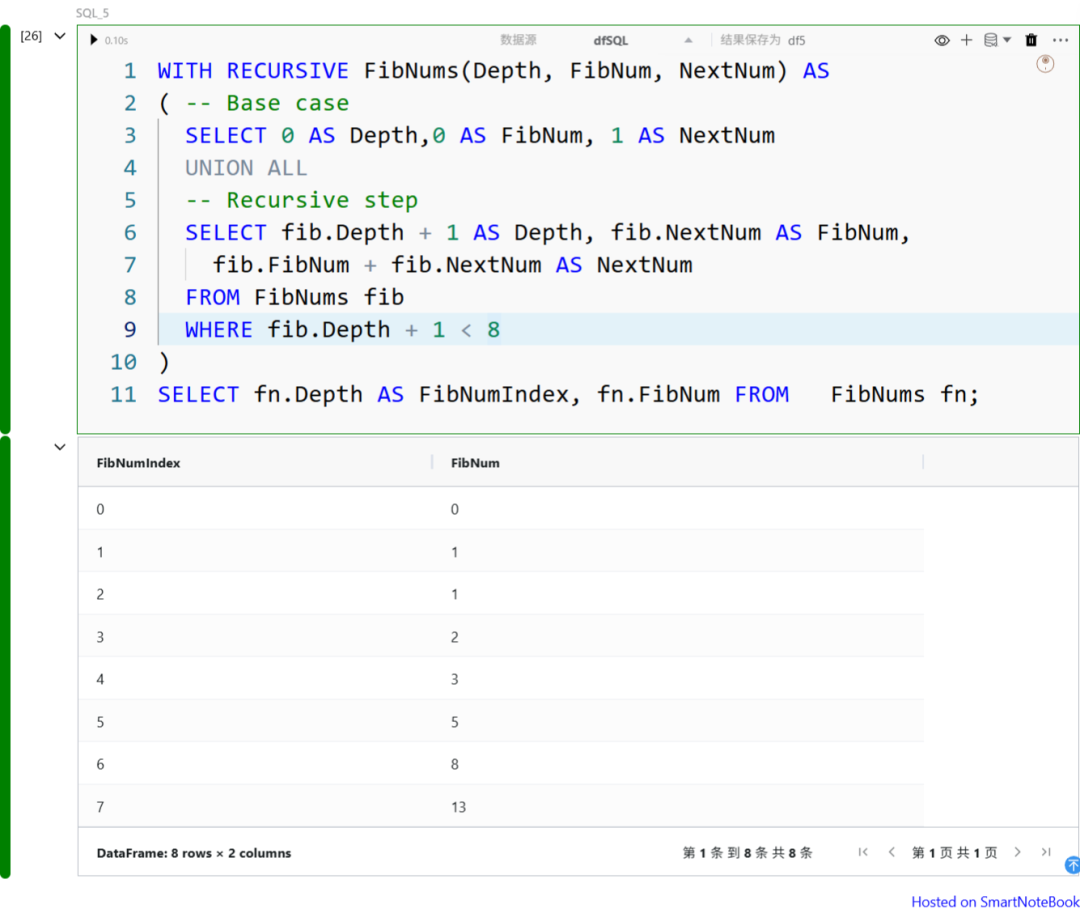
WITH RECURSIVE 不仅可以用于构造数字序列,还可以实现更复杂的递归计算。比如,我们可以利用它来生成前 8 个斐波那契数:
 图片
图片
示例:树结构遍历(Tree Traversal)
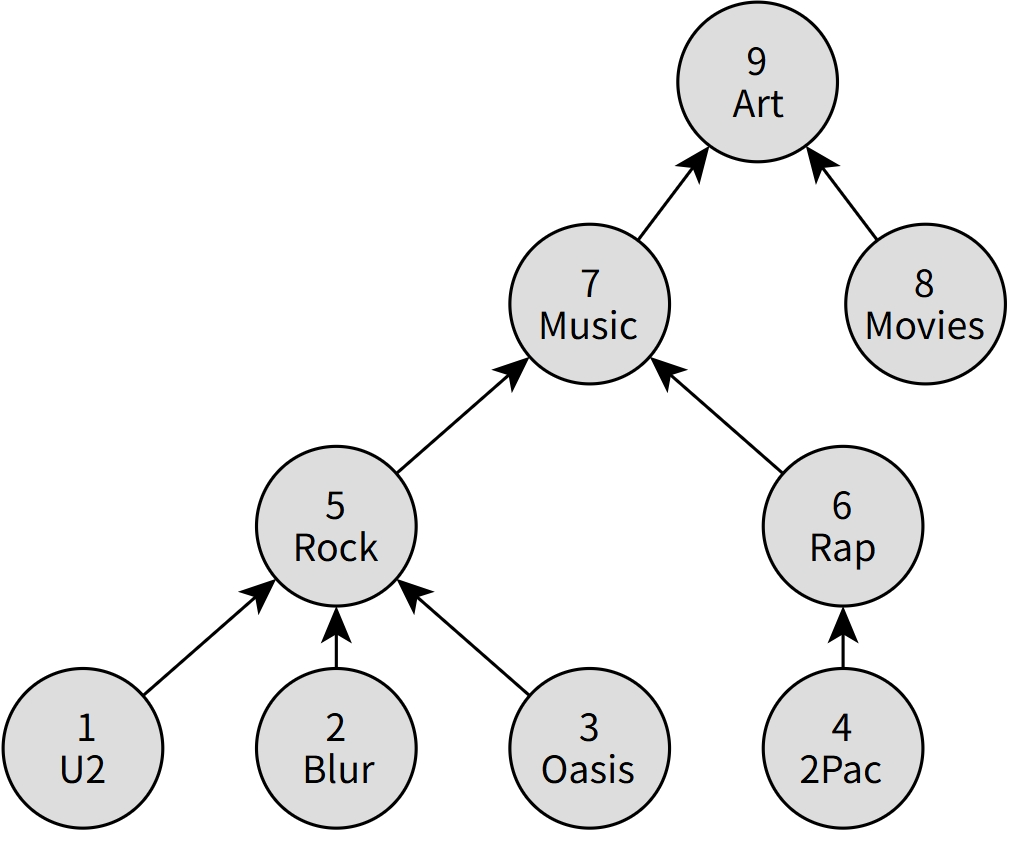
除了计算数值,WITH RECURSIVE 还可以用于遍历树形结构,这在处理层级数据(如组织架构、分类标签、菜单结构等)时非常常见。
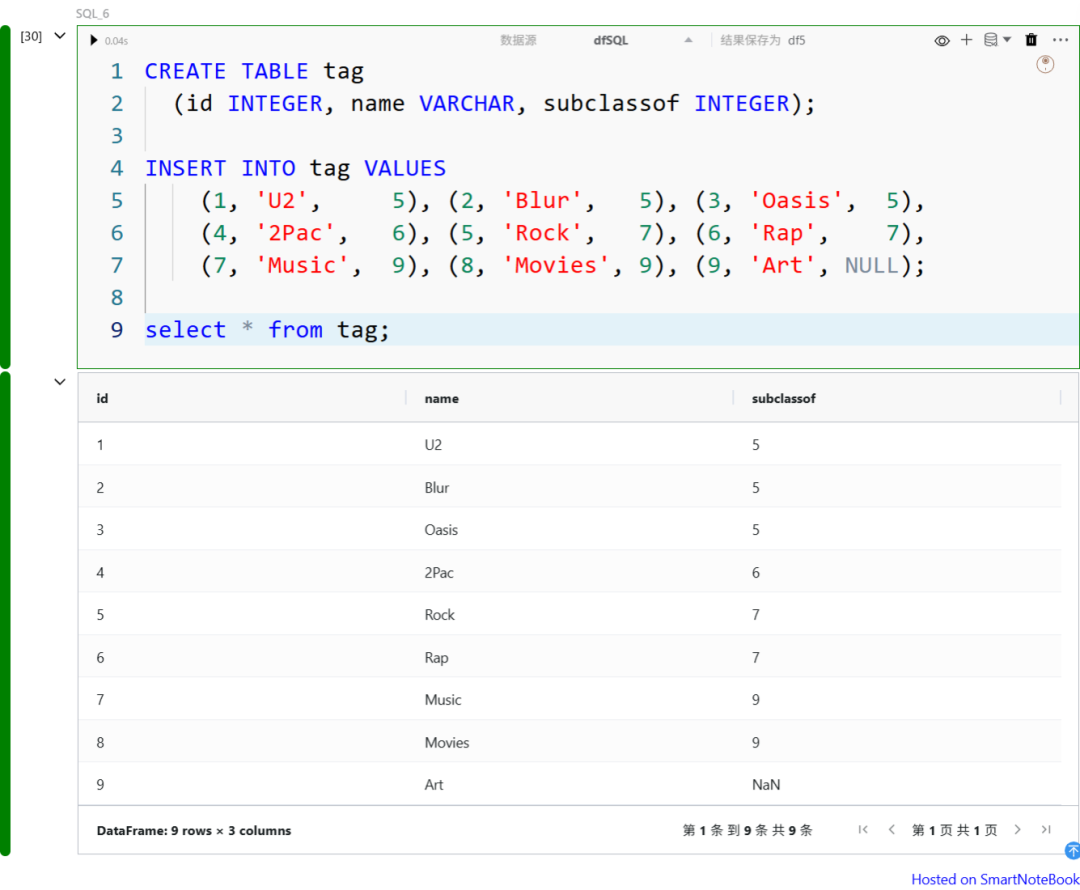
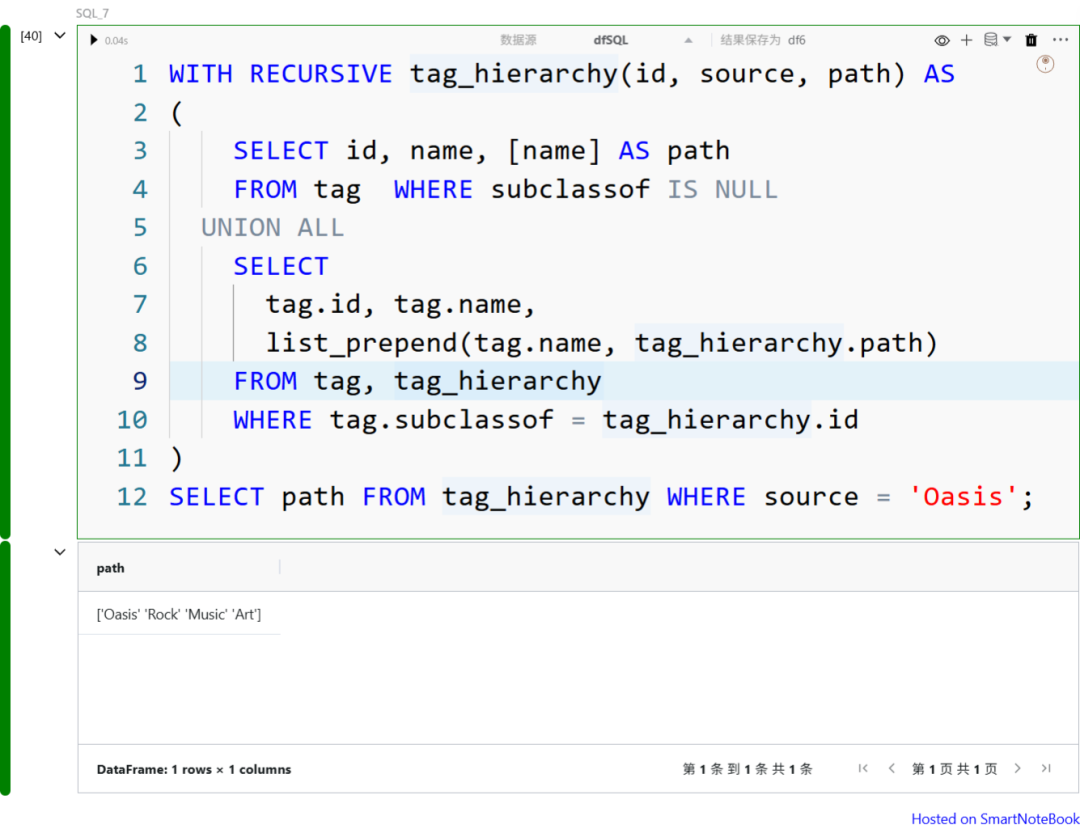
比如,下面是一个“标签(tags)层级结构”的递归遍历案例:
 图片
图片
 图片
图片
 图片
图片
示例:图遍历(Graph Traversal)
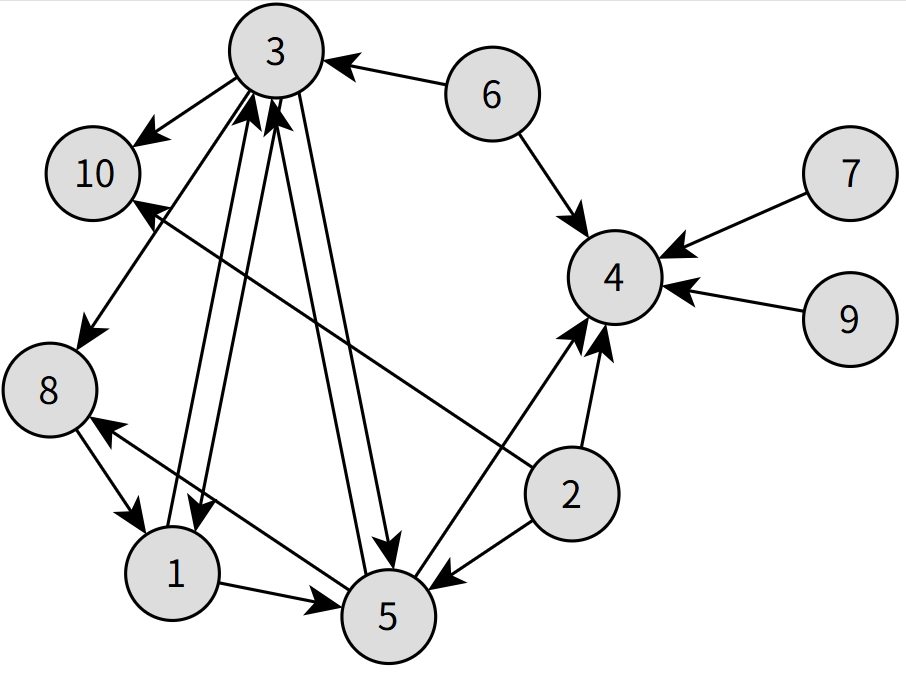
借助 WITH RECURSIVE,我们甚至可以在 SQL 中实现任意图结构的遍历(Graph Traversal)。这对于表示如路线网络、依赖关系图、社交图谱等复杂结构非常有用。
不过需要特别注意的是:如果图中存在环(cycle),就必须进行循环检测,否则递归查询可能会陷入死循环,永远无法终止。
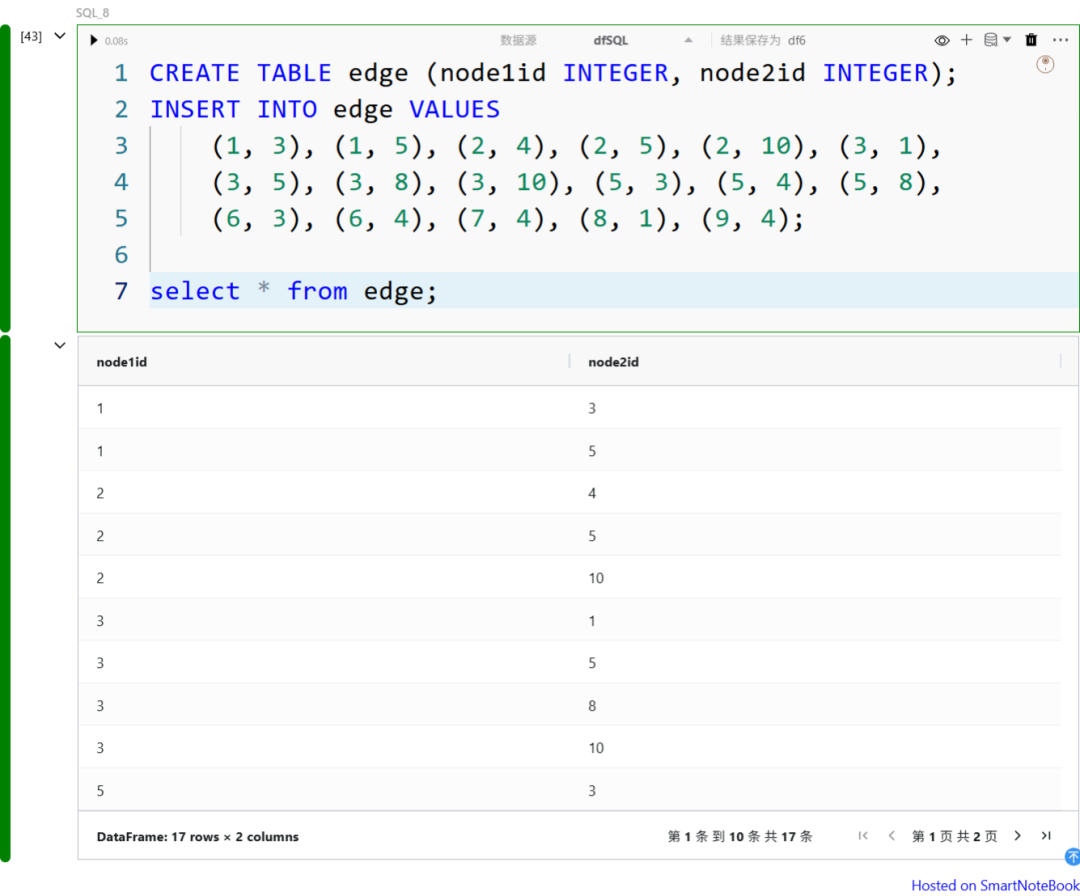
一种常见的做法是:在递归过程中记录当前路径,每次延伸路径前,先检查目标节点是否已访问过,从而避免重复走回头路。下面的示例中详细演示这一做法。
 图片
图片
 图片
图片
需要注意的是,这类图结构中可能包含有向环(directed cycles),比如节点 1、5 和 8 之间就形成了一个闭环。
枚举从某个节点出发的所有路径(Enumerate All Paths from a Node)
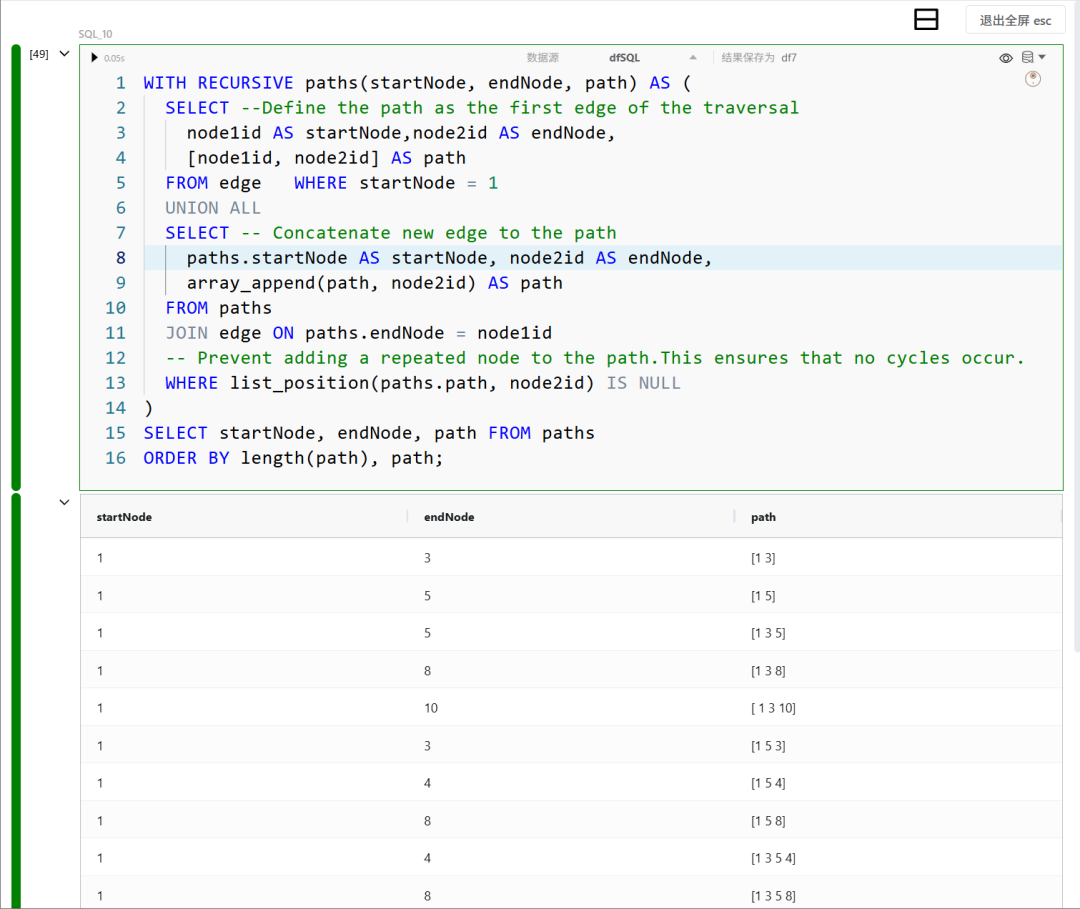
下面这个查询展示了如何使用 WITH RECURSIVE 来枚举从节点 1 出发的所有路径:
 图片
图片
需要注意的是,这个查询的结果并不限于最短路径。
例如,对于节点 5,结果中既包含直接路径 [1, 5],也包含更长的路径 [1, 3, 5]。
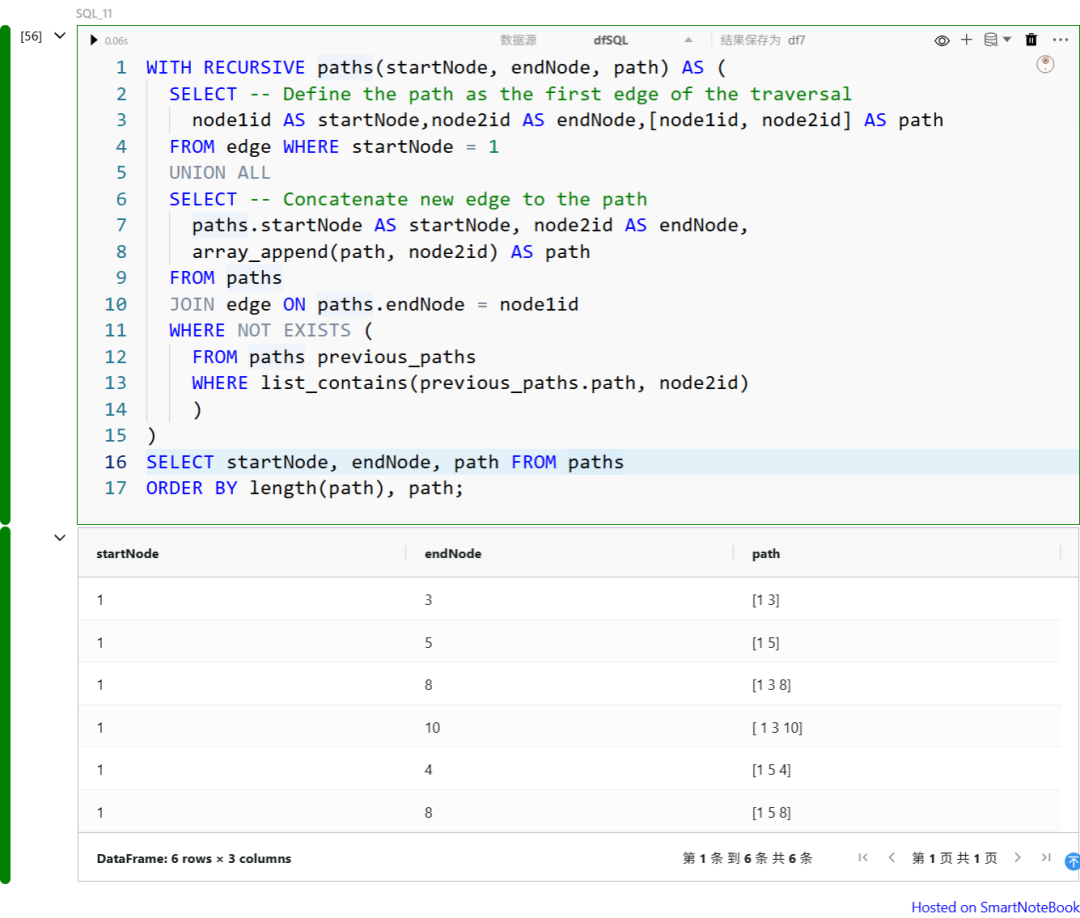
换句话说,它会列出所有可能走通的路径,而不是只保留最短的那一条。如果你希望过滤最短路径或添加路径权重,还需要进一步处理。
 图片
图片
枚举两个节点之间的无权最短路径(Enumerate Unweighted Shortest Paths)
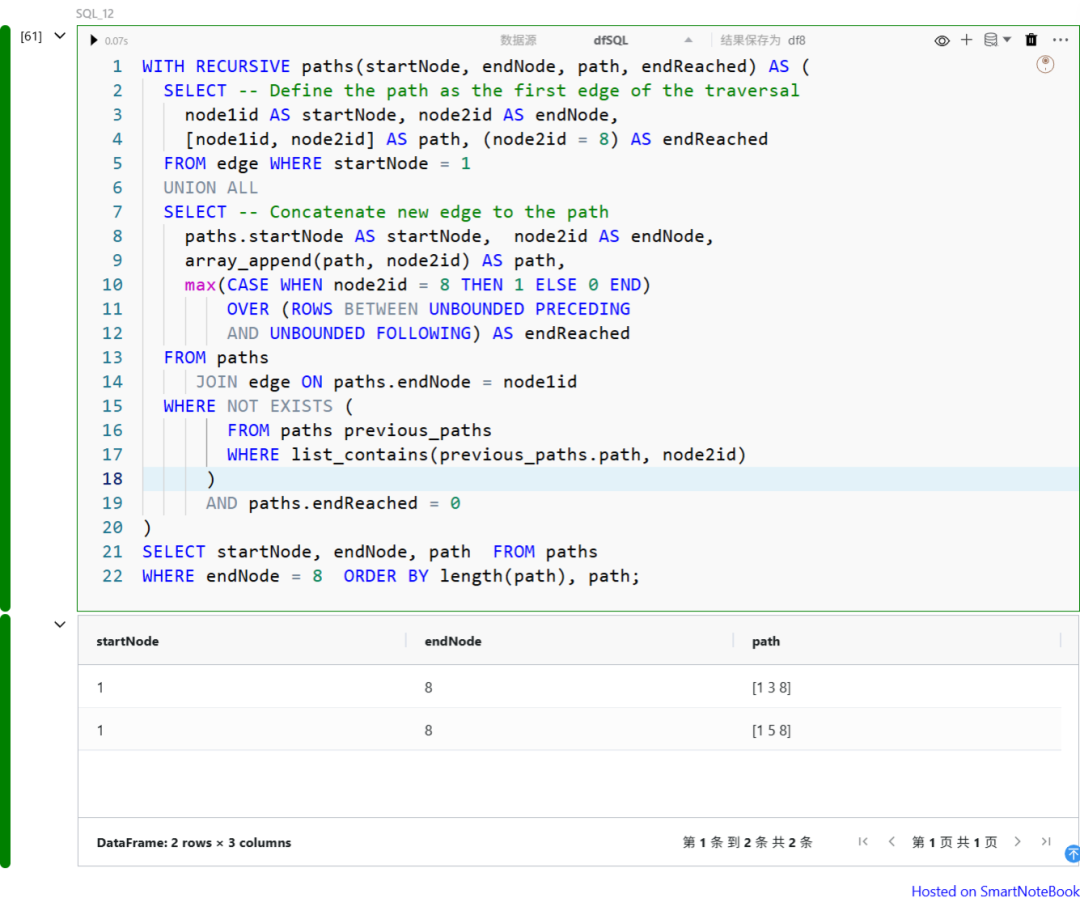
WITH RECURSIVE 还可以用来查找两个节点之间的所有无权最短路径。为了保证递归查询在到达目标节点后及时终止,我们可以借助窗口函数,检查当前新增节点中是否已包含目标节点。
下面的查询展示了如何找出从节点 1(起点)到节点 8(终点)之间的所有无权最短路径:
 图片
图片
递归不仅属于编程语言,SQL 也能“递归”!借助 WITH RECURSIVE,我们可以优雅地处理数字序列、树结构、图遍历等复杂问题。无论是层级查询,还是路径搜索,Recursive CTE 都是一种强大且灵活的利器。












