【2024美赛C题】O奖论文翻译 2401298 一个双时间贝叶斯网络模型
目录
1.1 问题背景
1.2 澄清与重述
1.3 我们的工作
2.1 模型假设
2.2 符号说明
2.3 数据清理
3 问题 1：概率差评估策略
3.1 发球方的重要影响
3.2 滑动点数区间方法
4 问题 2：势头存在性
4.1 假设检验准备
4.2 Ljung-Box Q 检验和游程检验统计分析
4.3 瞬时胜率
5.1 基础构建块：朴素二项模型
步骤 1：似然函数
步骤 2：对数似然
步骤 3：对所有比赛的对数似然求和
步骤 4：最大化对数似然
5.2 作为残余效应的势头
5.2.1 变量识别
5.2.2 模型构建
5.2.3 数据拟合
5.2.4 对比赛数据的推断
5.2.5 建议
7.1 优点与缺点
优点：
缺点：
7.2 敏感性分析
7.3 结论
8 备忘录
摘要
本研究通过复杂的统计建模和新颖的双时间贝叶斯网络方法探讨网球比赛的动态。通过分析温网数据，我们解决了五个关键问题：
表现指标（问题1）： 我们引入了一个发球方/接发球方的重新加权策略来准确评估球员的表现。我们进一步利用滑动窗口和曲线下面积（AUC）方法来确保连续性和局部性，从而更好地捕捉比赛中的波动。
势头存在性（问题2）： 严格的假设检验（Ljung-Box Q 检验和游程检验）未能拒绝完全随机性的原假设。但瞬时胜率可以揭示与随机性的轻微偏离，表明存在微妙的势头效应，尽管并非压倒性结论。
势头预测（问题3）： 我们采用两步法。首先，通过将势头效应视为朴素二项模型残差的方式将其分离出来。随后，我们开发了一个双时间贝叶斯网络模型来预测这种残余效应。该网络融合了各种潜在变量，如生理状态、感知和控制感、自我效能等。该模型的另一个成果是通过信息熵的减少来计算各因素对势头的重要性。
预测分析（问题4）： 我们的模型在 2023 年温网比赛中进行了测试，成功预测了大部分比赛波动。我们分析了失败的实例并提出了未来潜在的改进方案。该模型框架也应用于一个额外的女子网球比赛数据集，揭示了有趣的差异。最重要的是，我们将我们的数据推广成一个用于预测体育比赛中势头的通用框架。
教练策略（备忘录）： 最后，我们为教练起草了一份备忘录，将我们的发现综合成统计结论和针对性建议，包括最小化失误、策略性进攻、韧性培养等。我们的目标是提供竞争优势。
我们的发现凸显了网球比赛动态的复杂性，将严格的统计验证与复杂的预测建模相结合。我们的模型不仅展示了有效的预测能力和显著的鲁棒性，而且广泛适用于各种体育场景。
关键词： 网球，势头，贝叶斯网络，统计分析，表现指标。
===== 第 2 页 =====
1 引言 3
1.1 问题背景 3
1.2 澄清与重述 3
1.3 我们的工作 3
2 建模准备 4
2.1 模型假设 4
2.2 符号说明 4
2.3 数据清理 5
3 问题1：概率差评估策略 5
3.1 发球方的重要影响 5
3.2 滑动点数区间方法 6
3.3 滑动时间窗口方法 7
4 问题2：势头存在性 8
4.1 假设检验准备 8
4.2 Ljung-Box Q 检验和游程检验统计分析 9
4.3 瞬时胜率 10
5 问题3：势头预测 11
5.1 基础构建块：朴素二项模型 11
5.2 作为残余效应的势头 12
5.2.1 变量识别 13
5.2.2 模型构建 15
5.2.3 数据拟合 17
5.2.4 对比赛数据的推断 19
5.2.5 建议 19
6 问题4：波动预测与模型泛化 20
7 模型分析 22
7.1 优点与缺点 22
7.2 敏感性分析 22
7.3 结论 23
8 备忘录 23
参考文献 25
===== 第 3 页 =====
1 引言
1.1 问题背景
2023 年温网卡洛斯·阿尔卡拉斯对阵诺瓦克·德约科维奇的历史性比赛，揭示了势头在网球中的深远影响。这场比赛不仅吸引了网球爱好者，也凸显了竞技体育中一个复杂但尚未充分探索的方面：球员通过“势头”改变比赛动态的能力。势头在决定比赛结果中的重要性已成为一个关键的兴趣领域。排球运动员甚至利用这一点进行分配决策。这强调了对一个捕捉势头本质并解释其基本原理的复杂模型的需求。
1.2 澄清与重述
我们的任务围绕开发一个可量化的网球势头模型展开，该模型旨在识别势头转变的关键指标，评估其对比赛结果的影响，并辨别这些转变在多大程度上可归因于技能、策略或仅仅是运气。我们将执行以下步骤：
-
创建一个描述网球比赛进程、量化球员随时间表现的模型。
-
构建一个假设检验框架，以评估比赛中的波动是由于势头还是仅仅是运气。
-
使用我们的模型预测比赛动态的变化，识别可能预示比赛转变的潜在指标。
-
在各种比赛、场地类型以及可能其他类似运动中测试我们模型的预测能力，评估其泛化性。
-
将我们的发现综合成可供教练采取行动的策略，帮助他们在赛前为球员应对比赛动态转变做好准备，并在比赛中有效应对势头变化。
1.3 我们的工作
为应对这一挑战，我们的方法将统计分析、机器学习技术和动态模拟交织在一起，构建了一个全面的网球势头模型。通过仔细分析精选比赛的数据，我们试图找出标识势头转变的模式和相关性。我们的方法包括一个严格的验证过程，确保模型在现实世界场景中的可靠性和适用性。通过这个创新的视角，我们旨在阐明利用势头的策略，从而丰富职业网球高风险环境中运动员和教练可用的战术库。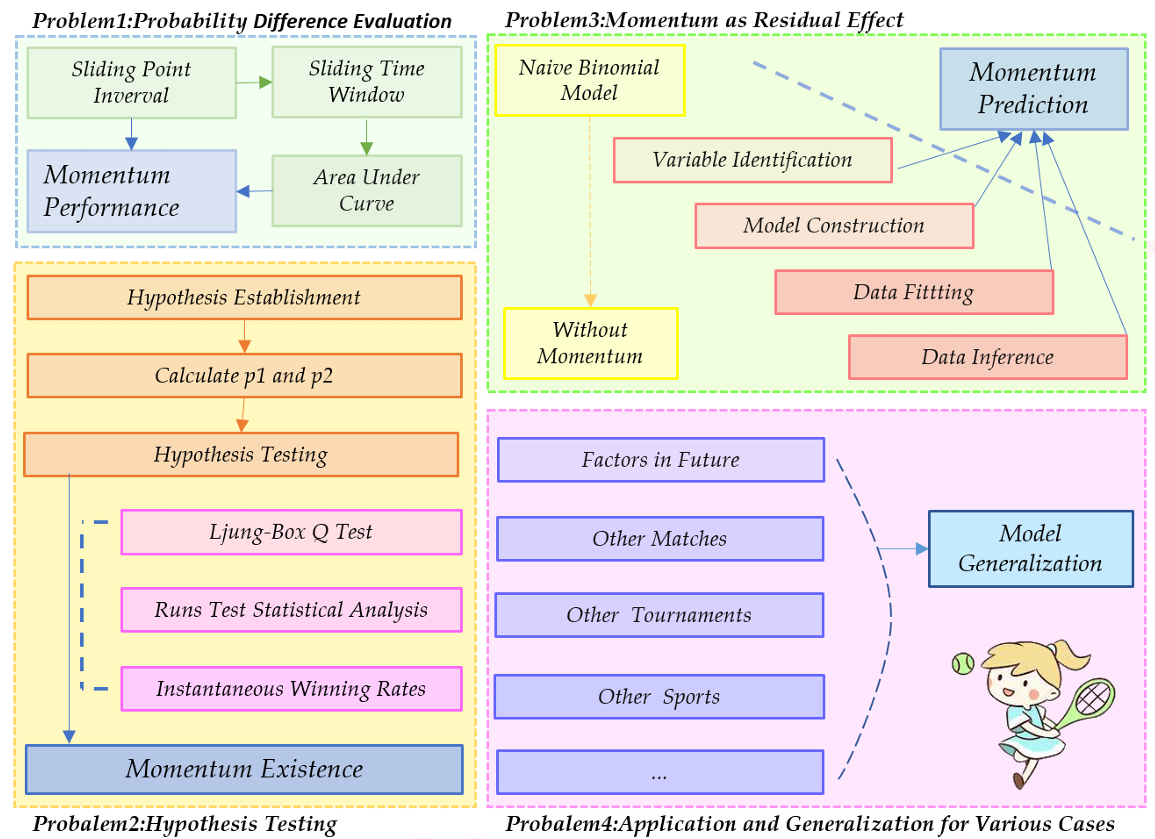
===== 第 4 页 =====
2 建模准备
2.1 模型假设
下面列出了一些基本假设。
-
假设 1： 天气、观众支持和轻微伤病等因素不会显著影响比赛结果。
-
理由： 虽然这些因素可能影响比赛，但将其纳入模型会增加复杂性和不可预测性。对于广泛的分析，专注于更可测量和一致的因素是实际可行的。
-
-
假设 2： 球员当前的世界排名是其即将到来的比赛中潜在表现的可靠指标。
-
理由： 排名基于球员在一定滚动周期内锦标赛的表现，反映了他们的整体能力。
-
2.2 符号说明
下面列出了一些主要符号。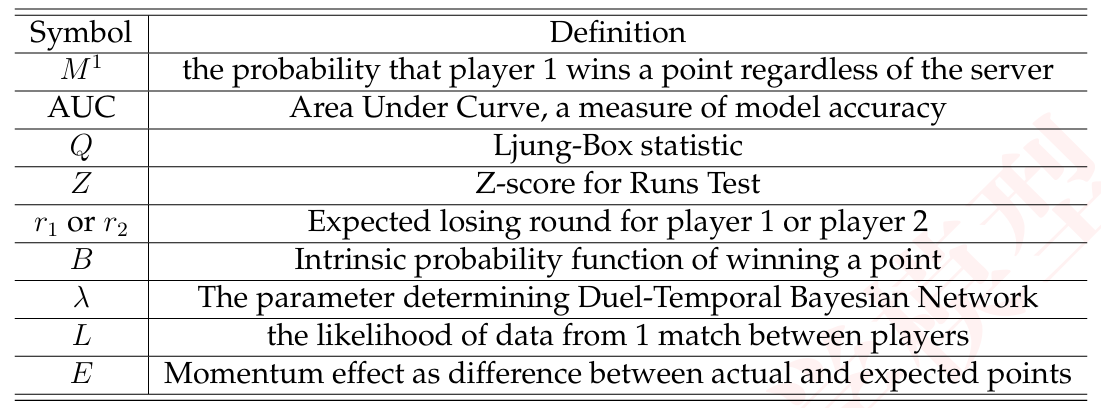
===== 第 5 页 =====
表 1：符号表
| 符号 | 定义 |
|---|---|
| M1 | 球员 1 赢得一分的概率（无论发球方是谁） |
| AUC | 曲线下面积，衡量模型准确性的指标 |
| Q | Ljung-Box 统计量 |
| Z | 游程检验的 Z 分数 |
| r1r1 或 r2r2 | 球员 1 或球员 2 的预期失利轮次 |
| B | 赢得一分的内在概率函数 |
| λλ | 决定双时间贝叶斯网络的参数 |
| L | 来自一场球员间比赛的数据的似然 |
| E | 势头效应，定义为实际得分与预期得分之差 |
2.3 数据清理
观察温网精选比赛数据 featured_matches.csv 后，我们处理了列 elapsed_time（第 586 至 636 行）中的异常值，并删除了 speed_mph 列，因为其中缺失值数量较多，可能影响整体分析。
3 问题 1：概率差评估策略
3.1 发球方的重要影响
让我们考虑比赛中球员 1 和球员 2 之间得分差的变化，根据温网 featured_matches.csv 数据集，我们从 p1_points_won 数据中减去 p2_points_won 得到得分差，即：
得分差=p1_points_won−p2_points_won(1)
这个公式帮助我们可视化比赛进程，如下图所示，它突出了得分差随时间的变化：
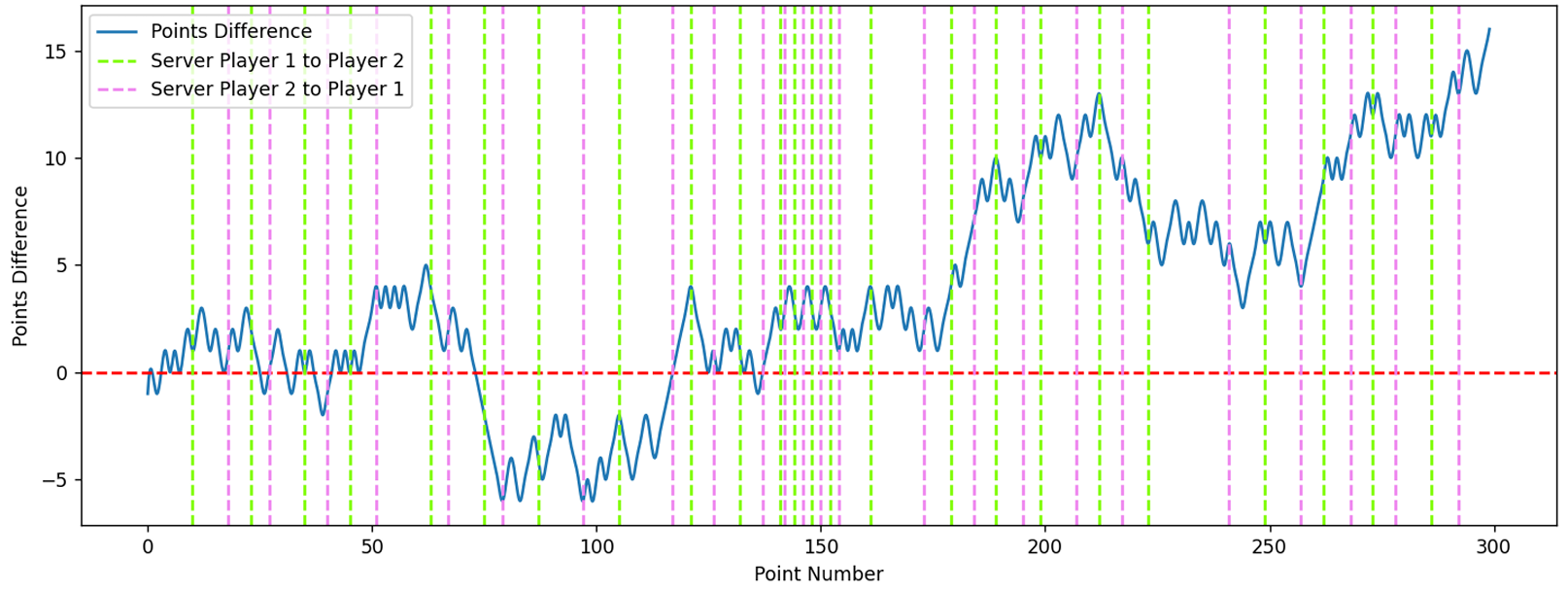图 2：比赛 2023-wimbledon-1301 的得分差
图中还添加了两条彩色虚线：绿色表示由球员 1 发球给球员 2，紫色表示由球员 2 发球。
===== 第 6 页 =====
一个关键的观察是，当前发球的球员有更高的机会赢得这一分，特别是当点数在 [20,50][20,50] 或 [180,220][180,220] 区间时。然而，无论谁发球，得分差的总体趋势保持相对稳定，表明仅靠发球并不能极大地改变比赛势头。因此，当我们试图识别在比赛给定时间哪个球员表现更好时，不能被谁是发球方所影响。
3.2 滑动点数区间方法
为了进一步分析比赛动态，我们关注球员赢得一分的概率差。在一场比赛中，两名球员的表现取决于概率差 M1 或 M2，其中 M1 是球员 1 赢得一分的概率（无论发球方是谁），M2 是球员 2 赢得一分的概率（无论发球方是谁）。
接下来，根据给定数据集中的 point_no 列，我们可以通过选择一个固定长度 ω 的数据来计算 p1 和 p2，其中 p1 是球员 1 在发球时赢得一分的概率，p2 是球员 2 在发球时赢得一分的概率，ω 是点数区间。如果球员 1 发球 n1 次，球员 2 发球 n2 次（其中 w=n1+n2），球员 1 赢得 x1 分，球员 2 赢得 x2 分，那么 p1=x1/n1和 p2=x2/n2。实际上，我们可以得到表现指标：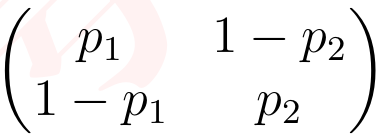
。如果球员 1 和球员 2 有相同的发球机会，p1p1 和 p2p2 的理想值应该相等，那么
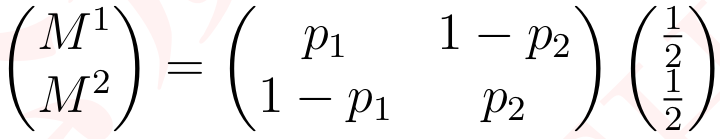(2)
当 M1>0.5时，意味着球员 1 表现优于球员 2，而当 M1<0.5时则相反。此外，该值越高，表明球员 1 表现越好，因此它可以识别在比赛给定时间哪个球员表现更好，以及他们表现好多少。
为了可视化球员 1 和 2 的不同表现，我们引入一个长度为 ω 的滚动窗口。对于每场比赛，我们可以利用这个“滚动窗口”来计算球员 1 和球员 2 之间的表现差异，并结合三次样条插值，我们可以绘制相应的表现程度变化曲线，并画出以下曲线（ω=30）：
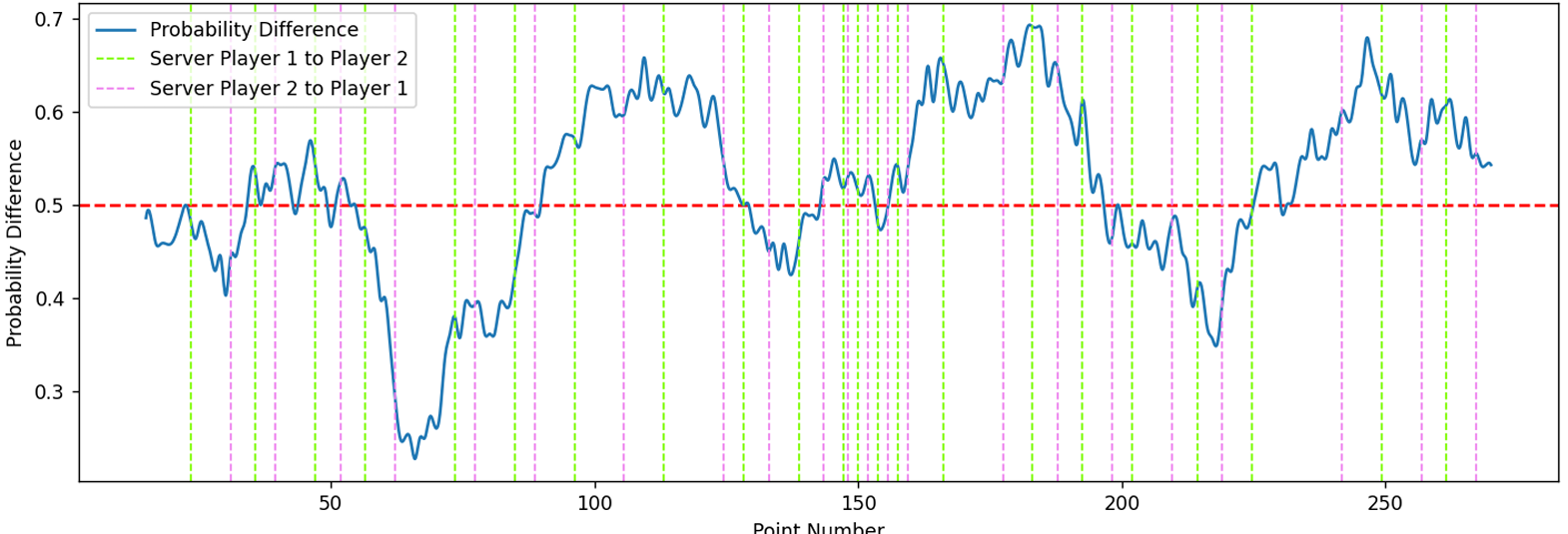
图 3：比赛 2023-wimbledon-1301 的概率差
其中横坐标是比赛中得分的总点数（当两名球员完成一次击球时加1，对应于给定数据中的point_no列），纵坐标表示概率差 M1。与图2相比，我们发现发球方的变化与概率差无关，这意味着比较概率差比比较得分差更为显著。
从图3来看，红色线上方的部分表明球员1（卡洛斯·阿尔卡拉斯）优于球员2（尼古拉斯·贾里），红色线下方的部分则表明球员2（尼古拉斯·贾里）优于球员1（卡洛斯·阿尔卡拉斯）。此外，波峰和波谷的位置表明该球员在相应时段表现尤为出色。
3.3 滑动时间窗口方法
然而，仅根据总得分的均匀区间选择数据点进行绘制是不够的，我们还应该从比赛时间的角度进行均匀分割。记 L 为时间窗口的长度，λ 为每个时间窗口移动的步长。将点数替换为 ti 作为横坐标，ti=λ秒,2λ秒,...。例如，如果使用 L=600秒作为时间窗口的长度，两名球员可能总共打了12分或18分，然后设定 λ=60秒 作为时间窗口移动的步长，这样得到的结果更能反映球员的表现，也更自然。
通过调整不同的 L 和 λ，我们绘制出如下变化图：
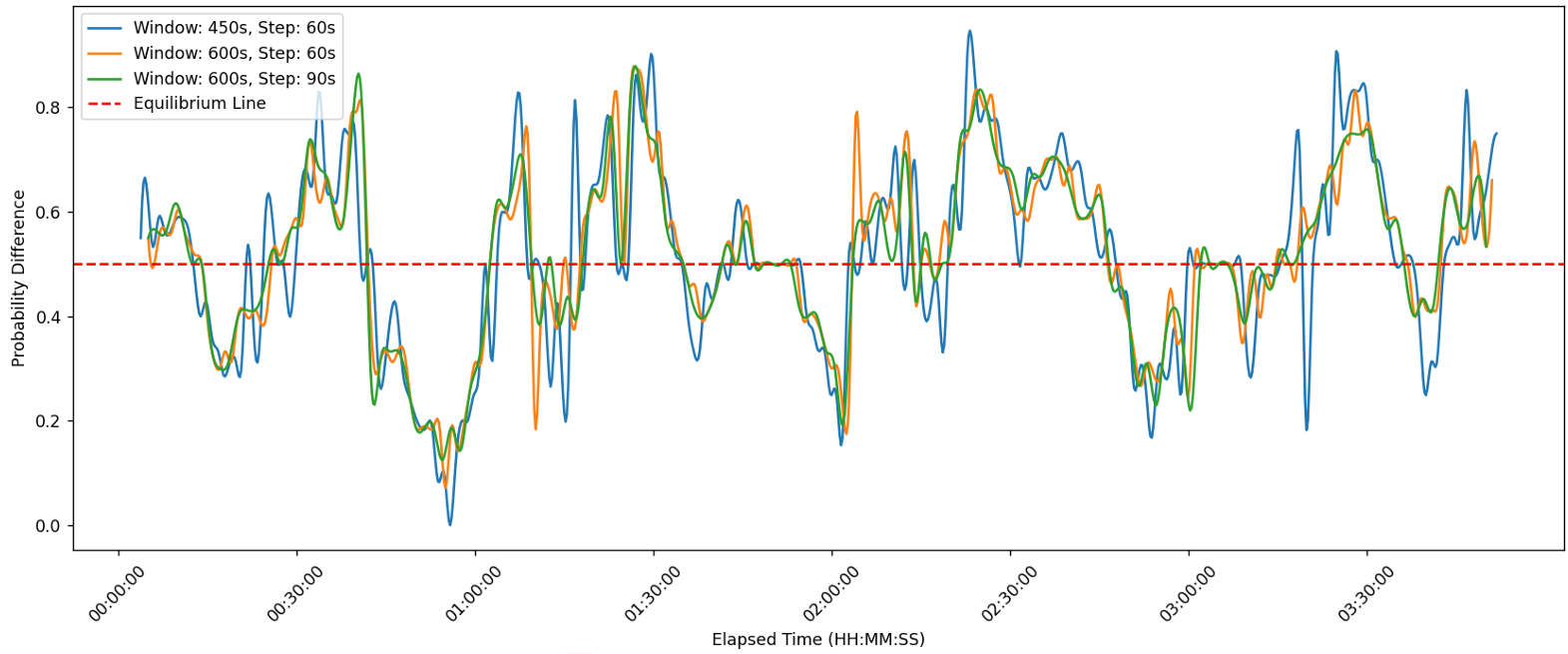
图4：针对比赛 2023-wimbledon-1301 使用不同窗口的性能评估
我们可以从图中观察到，球员在某些时刻的表现受到时间窗口长度 L的显著影响，而受时间窗口移动步长 λ的影响较小。一般来说，小窗口会引入噪声，而大窗口则无法描绘比赛的快速变化动态。为了解决这个问题，一种常见的方法是应用滤波器，如高斯滤波器，这需要一个特定的核函数。这需要修改公式2。但我们在此提出一个更简单且同样有效的方法，称为 AUC（曲线下面积），其定义如下公式所示：
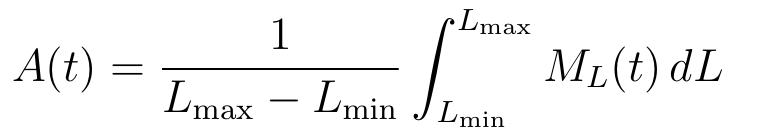（3）
===== 第 7 页 =====
其中 ML(t) 表示在考虑窗口长度 L 时，某一球员在时间 t的表现。在实际操作中，我们可以简单地将 dL 离散化为 1。与基于核函数的方法类似，AUC 方法也根据时间距离对得分进行加权（这可以通过将 ML(t) 表示为指示函数之和，然后交换求和顺序来轻松看出，我们在此省略细节）。以下是使用此方法生成的图形。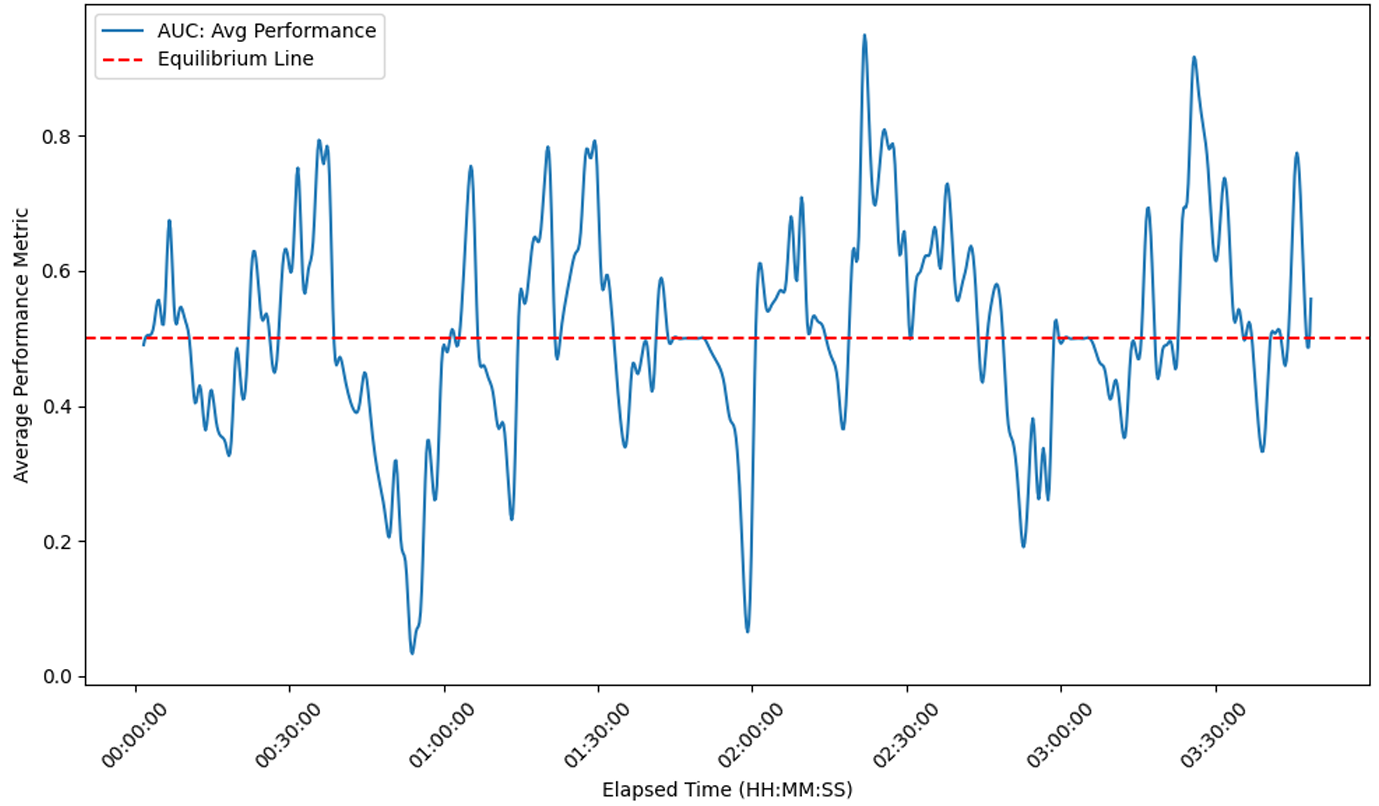
图 5：比赛 2023-wimbledon-1301 的 AUC-时间图
从这个图中，我们可以确定在特定时间哪个球员表现更好。当曲线高于 0.5 时，球员 1 占据上风，而当球员 2 表现更好时则相反。曲线距离均衡线越远，球员之间的表现差异就越大。
4 问题 2：势头存在性
鉴于我们的分析揭示了“势头”中的潜在模式，我们现在通过假设检验严格审视这些观察结果，以验证势头的存在。
4.1 假设检验准备
我们首先构建了假设检验框架：
-
原假设 (H0)：对于一个固定的发球方，球员的得分是独立同分布的（i.i.d.），因此服从二项分布。
-
备择假设 (H1)：H0H0 的补集，表明得分并非完全随机，存在某种形式的“势头”或序列依赖性。
为了评估关于“势头”不存在的说法，我们指出在任何给定的比赛中，当球员 1 发球时，球员 1 赢得一分的概率为 p1，当球员 2 发球时，球员 1 赢得一分的概率为 p2。这些概率 p1 和 p2p 的计算在第 3 节中说明。
对于每场比赛，我们通过以下方式计算获胜概率：通过统计球员 1 赢得的分数和球员 1 的总发球次数来计算 p1以及球员 1 对阵球员 2 发球时赢得的分数与球员 2 总发球次数的比值来计算p2。
4.2 Ljung-Box Q 检验和游程检验统计分析
如果得分完全随机，我们预计连续得分之间没有显著的自相关性。
我们分离出球员 1 发球和球员 2 发球的情景，并为每场比赛构建序列。然后计算每个序列的自相关性，并采用适当的统计检验（Ljung-Box Q 检验）来评估序列的自相关性是否显著。
Ljung-Box Q 检验的统计量计算如下：
(4)
其中：n 是时间序列的样本大小。h是为自相关性检测考虑的最大滞后数。ρ^k 是滞后 k 处的样本自相关系数。Q 是 Ljung-Box 统计量，在原假设下近似服从自由度为 h−m 的卡方分布，其中 mm 是模型中的参数数量（对于简单时间序列分析，通常取 m=0）。
第一场比赛的 Ljung-Box Q 检验结果，对应的 p 值为 0.497（对于最多 10 个观测值的自相关性），表明 p 值大于常见的显著性水平（例如 0.05）。其他比赛的结果类似。这表明没有足够的证据拒绝原假设 H0。
然后我们进行了游程检验来分析数据序列中“游程”的数量，其中“游程”定义为连续出现的相同元素序列。我们计算了预期游程数和方差，并通过以下公式得到 Z 分数：
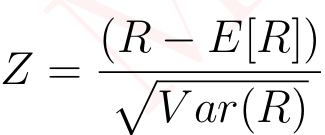(5)
其中：R 表示实际的游程数。E[R] 是预期的游程数，计算为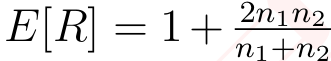 
。Var(R)是游程数的方差，计算为 
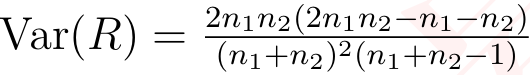。n1 和 n2 是序列中两种结果（例如，赢和输）的计数。
然后我们通过以下公式计算 P 值：P=2(1−Φ(∣Z∣))，得到 P=0.691，该值大于常见的显著性水平（例如 0.05），表明得分是独立同分布的这一假设不能被拒绝。其他比赛的结果类似。
这里我们绘制了两种方法在不同比赛中的结果。正如除少数几场比赛外，各场比赛的 PP 值均超过 0.05 基准所证明的那样，对于大多数比赛，我们不能拒绝 H0。
图 6：特征重要性
4.3 瞬时胜率
为了检验独立同分布的论点，受论文 [Sun, Y., 2004] 的启发，我们采用了瞬时胜率方法。该胜率指的是在发球方恒定的条件下，球员在赢得一分后立即赢得下一分的概率。我们计算并比较了两种情景下的瞬时胜率：球员 1 在发球时赢得一分后立即赢得下一分的概率，以及球员 1 在面对球员 2 发球时赢得一分后立即赢得下一分的概率。
表 2：基于发球状态的获胜概率
| 球员和状态 | 发球时的获胜概率 | 非发球时的获胜概率 |
|---|---|---|
| 球员 2 | 0.6874 | 0.3406 |
| 球员 1 (即时后) | 0.6978 | 0.3498 |
| 球员 2 | 0.6594 | 0.3126 |
| 球员 2 (即时后) | 0.6683 | 0.3261 |
观察到的胜率大约增加 1% 可能表明了势头的影响，挑战了网球比赛中得分序列随机性的说法。
深入探究比赛数据的细微差别揭示了一个有趣的模式：无论是在发球还是接发球时，球员在赢得一分后，赢得下一分的概率都有小幅增加。虽然数据并未压倒性地支持势头的概念，但它确实没有否定其存在。
===== 第 10 页 =====
5 问题 3：势头预测
5.1 基础构建块：朴素二项模型
在竞赛中识别“势头”的一个直接问题是，我们观察到的所有变量都混合了势头效应和球员技能水平差异带来的效应。为了“分离出”势头效应，我们首先开发了一个不考虑任何势头的朴素模型。或者，等价地说，一个假设赢得的分是独立同分布随机变量的模型。我们将这个模型称为二项模型，记为 BM[5]。
为了开发这个模型，我们收集了球员的世界排名作为额外的先验信息...并将它们转换为 2023 年温网比赛的相对排名。通过“相对”，我们根据球员彼此之间的排名对 32 名球员进行重新排序，得到一个介于 1 和 32 之间的整数数组。那么 BM 就简单地是 (Rank1,Rank2)的函数。
我们的二项模型接受两名球员的排名，然后返回赢得某一分“内在概率”，在朴素假设下，这个概率在整个比赛中保持恒定。
值得注意的是，在网球比赛中，高排名球员之间的实力差异通常比低排名球员之间更明显。例如，我们可能预期排名第 1 和第 2 的球员之间的差异要大于排名第 31 和第 32 的球员之间的差异。相反，“预期失利轮次”的概念可以很好地捕捉这种先验信息。具体来说，我们定义
r1=6−log2(Rank1)(6)
相应地，我们可以定义 BM(Rank1,Rank2)≔f1(r1,r2)设 f2(x,y)=f1((x+y)/2,(x-y)/2)，我们有 BM=f2(r1−r2,r1+r2)。我们为 f2 提供了以下近似：
(7)
其中 s>0是发球优势。或者，我们可以将右侧设为 
并引入更多参数。
但在实验过程中，我们发现 mu的值相当小，因此在此忽略它。理想情况下，如果公式 (6) 已经足够好地捕捉了排名与实力的关系，那么这种简化是有意义的。更多理由请参考 [Klaassen and Magnus, 2001]。
然后，我们通过最大化似然函数，在 31 场比赛的逐点数据上估计参数 λ。
步骤 1：似然函数
假设各个得分的结果是独立的（我们朴素模型的一个假设），从一场球员 1 和球员 2 之间的比赛中观察到的数据的似然函数，其中球员 1 赢得 n1 分，球员 2 赢得n2 分，如下所示：
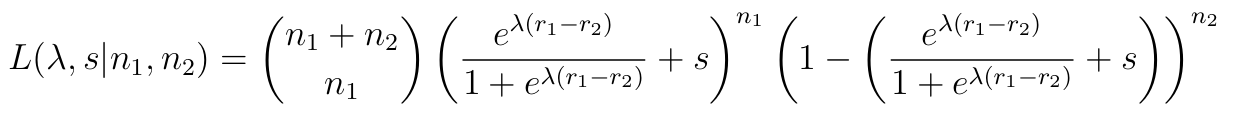(8)
步骤 2：对数似然
为了简化计算并处理潜在的数值下溢问题，通常使用对数似然而非似然本身。
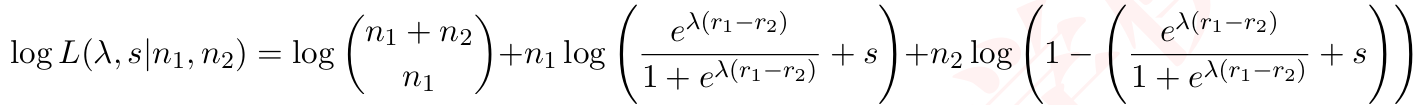(9)
步骤 3：对所有比赛的对数似然求和
为了使用所有 31 场比赛的数据估计 λ,sλ,s，我们对所有比赛的对数似然求和：
(10)
步骤 4：最大化对数似然
由于函数的平滑性，我们可以轻松应用牛顿法，该方法需要计算一阶和二阶导数，来迭代调整 λ,sλ,s 以找到最大值。计算出的最优值为 lambda = 0.0624, s = 0.1742。
5.2 作为残余效应的势头
我们很容易观察到“无势头”陈述与“无记忆”陈述的等价性。“势头不存在”⟺“赢得得分的过程与比赛的过去无关，或者换句话说，是无记忆的”。
现在，通过反转两边，我们可以将势头效应衡量为：
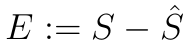(11)
其中 S 是实际赢得的分数，而 S^ 是二项模型预测的赢得的分数。由于势头作为一个统计量没有严格的定义。我们现在使用公式 (11) 来定义势头的值。这个公式可以直观地理解，因为先前对势头的批评常将其描述为“从随机性中看到了某种模式”。[4]
为了设计一个预测残差的模型，有几个关键事实值得注意：
-
“势头”之所以难以从统计上把握，是因为这个概念暗示了体育比赛系统中存在某种“隐藏状态”。因此生成模型是更可取的。
-
直接的单步预测可能极其嘈杂，因此对有效模型拟合构成挑战。我们需要特定的方法来减少噪声的影响。
-
过去比赛状态的影响应被编码到此模型中。并且过去的影响可能持续很长时间。
考虑到所有这些因素，我们引入了新颖的双时间贝叶斯网络。作为普通动态贝叶斯网络的变体，它不仅为网球比赛构建了一个隐藏模型，还编码了来自过去的长期和短期记忆，从而实现对“势头”的全面检测。
5.2.1 变量识别
在网球比赛中，看不见的因素可能与记分牌上的分数一样具有影响力。例如，球员表现的突然上升或下降并不总是来自可见的 Ace 球或双误。往往是隐藏的触发因素——也许是比赛的压力如何压在他们肩上——可以扭转局势。网球比赛不仅是力量或技巧的竞争，还涉及复杂的心理和生理动态。
根据 [Taylor J., 1994] 的见解，我们看到势头是一个由认知、生理和情绪组成的复杂系统，所有这些都由诱发事件引发并表现为绩效变化。这篇论文提出的“势头链”概念表明，初始事件可以引发运动员认知、情感和生理上的改变，导致影响绩效的行为变化，这与网球中起作用的看不见的力量产生共鸣，引导我们考虑潜在变量。
基于这个框架，我们在模型中选择 3 个潜在变量：“生理状态”、“控制感”和“自我效能感”。它们在捕捉影响网球比赛势头波动的复杂、不可观察因素方面起着关键作用。
-
生理状态： 球员的身体状况，如疲劳、能量水平，甚至轻微的伤病。
-
控制感： 这代表球员控制比赛的能力。
-
自我效能感： 自我效能感是球员对自己能力的信念，这是驱动球员坚持的动力。
根据 [Taylor J., 1994] 的研究，诱发事件，如特定的击球、关键得分，会间接改变球员的心理和生理状态。这些隐藏状态是比赛的暗流，看不见但至关重要。将它们纳入我们的模型可以更准确地理解和预测势头的波动。
然后我们得到下面的图示。下图中箭头代表各因素之间的影响关系。这个复杂的影响网络反映了竞技体育的多方面性质，其中身体、心理和情境因素都交织在一起影响比赛结果。
===== 第 14 页 =====
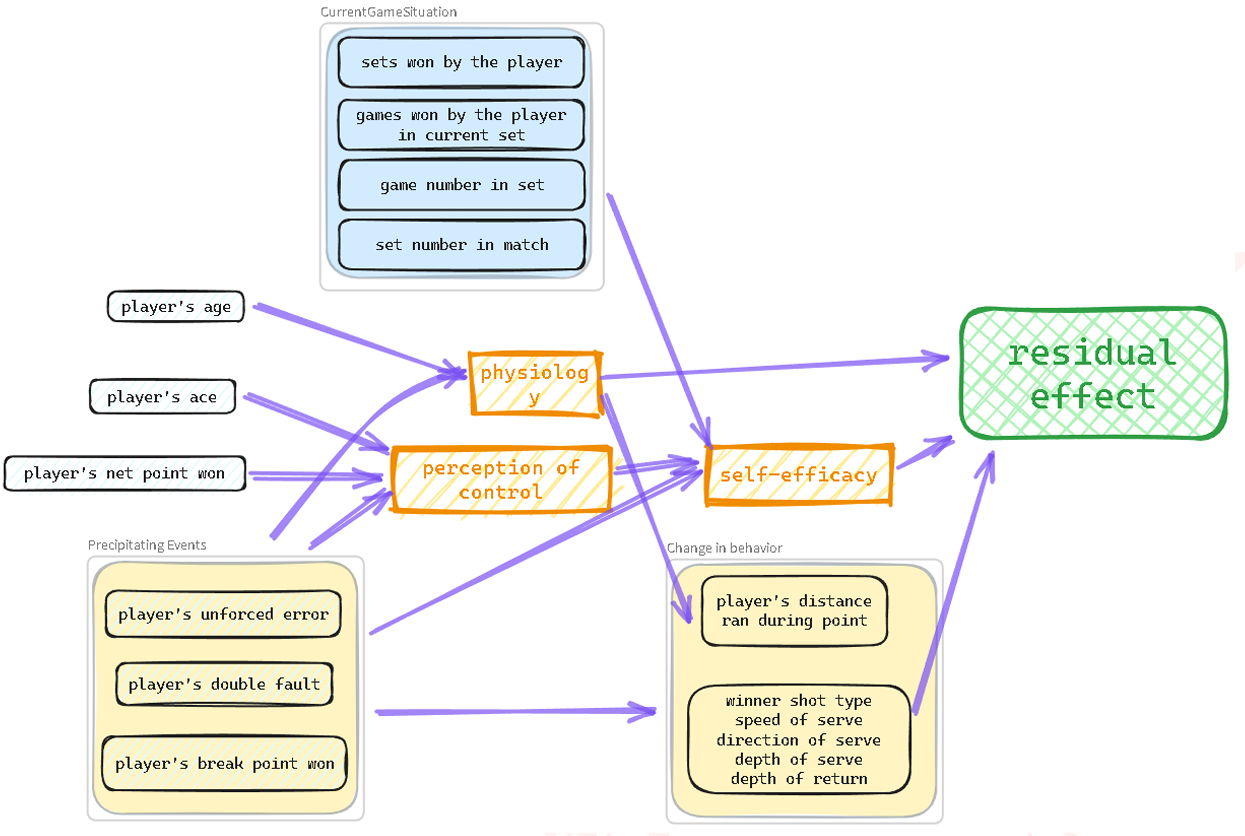
图 7：识别的变量
由于我们数据的限制（只有 31 场比赛），像这样复杂的模型容易过拟合，因此不适合用于鲁棒性预测。为了简化模型构建，我们利用随机森林来搜索对预测不重要的变量。以下是一些最重要的特征：
表 3：特征重要性
| 特征 | p1_unf_err | p2_winner | p2_unf_err | p1_winner |
|---|---|---|---|---|
| 重要性 | 0.120587 | 0.111018 | 0.101907 | 0.094330 |
| 特征 | server | rally_count | p2_net_pt_won | game_victor |
|---|---|---|---|---|
| 重要性 | 0.084700 | 0.081359 | 0.047800 | 0.043592 |
| 特征 | p1_net_pt_won | p2_distance_run | p1_distance_run |
|---|---|---|---|
| 重要性 | 0.032918 | 0.032348 | 0.032152 |
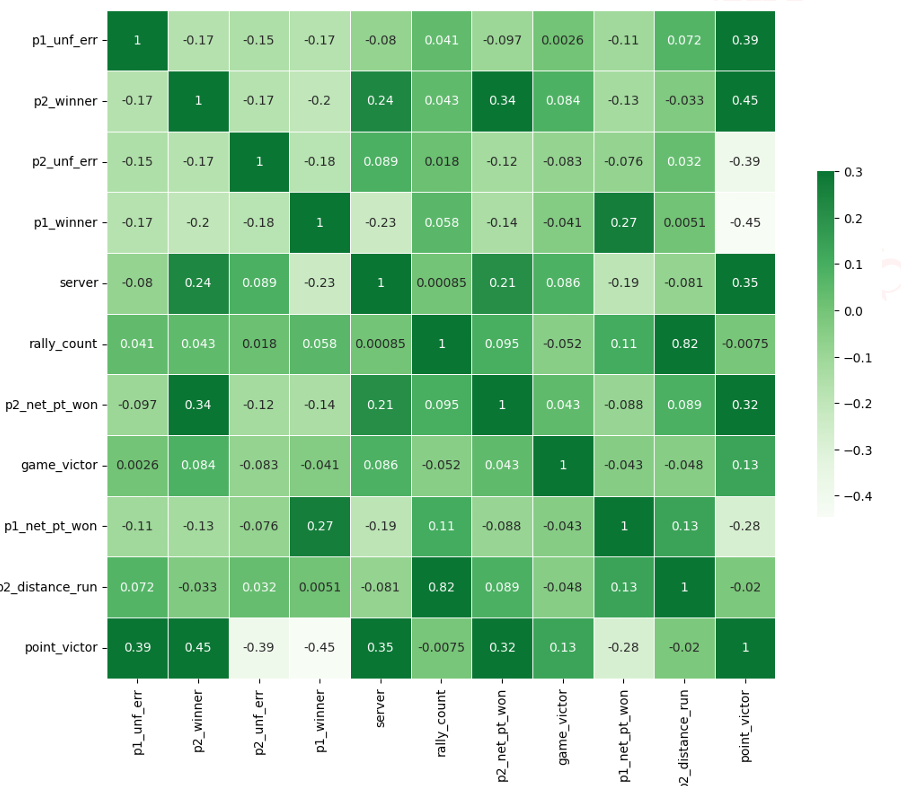
为了简化我们的网络，我们应该使用相关性热图可视化特征之间的相关性。这对于特征工程至关重要。前 10 个特征的相关性热图显示了与网球比赛得分获胜者最相关的变量之间的关系。以下是热图的一些见解：
-
非受迫性失误 (p_1 ext{unf_err}, p_2 ext{unf_err})：这些特征与得分结果显示出显著的相关性，意味着球员的错误可能对得分结果产生至关重要的影响。
-
制胜分 (p1winner,p2winner)：球员凭借制胜球赢得的分数与比赛结果高度相关。
-
发球（server）：发球方在一分中的作用具有显著的相关性与得分结果。
-
身体和策略方面（rally_count, p1_net_pt_won, p2_net_pt_won）：这些特征暗示了得分中涉及的身体消耗和策略性打法，例如更长的回合和成功的网前得分有助于得分结果。
这揭示了可能对势头做出贡献的比赛中的几个层面，例如直接影响，如非受迫性失误、制胜球，以及发球带来的优势。此外，像回合数和网前得分这样的身体和策略要素也可能影响球员在比赛中的主导地位。
5.2.2 模型构建
通过这种方法，我们确定并丢弃了不重要的特征，例如生理状态。剩余的特征构成了我们网络的基础。简化版本如下图所示：
===== 第 16 页 =====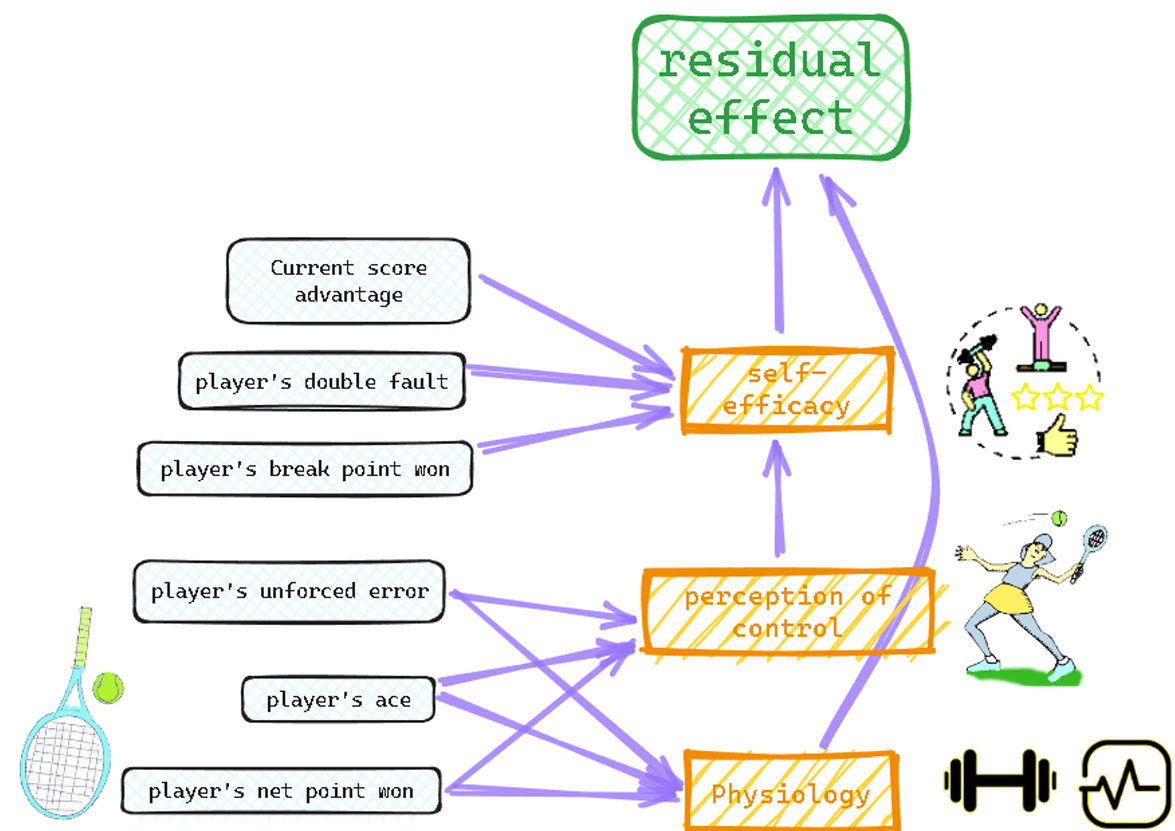
图 9：贝叶斯网络的一个构建块
使用这个更简单的网络作为一个构建块，我们可以将两个块堆叠在一起，形成我们的双时间贝叶斯网络：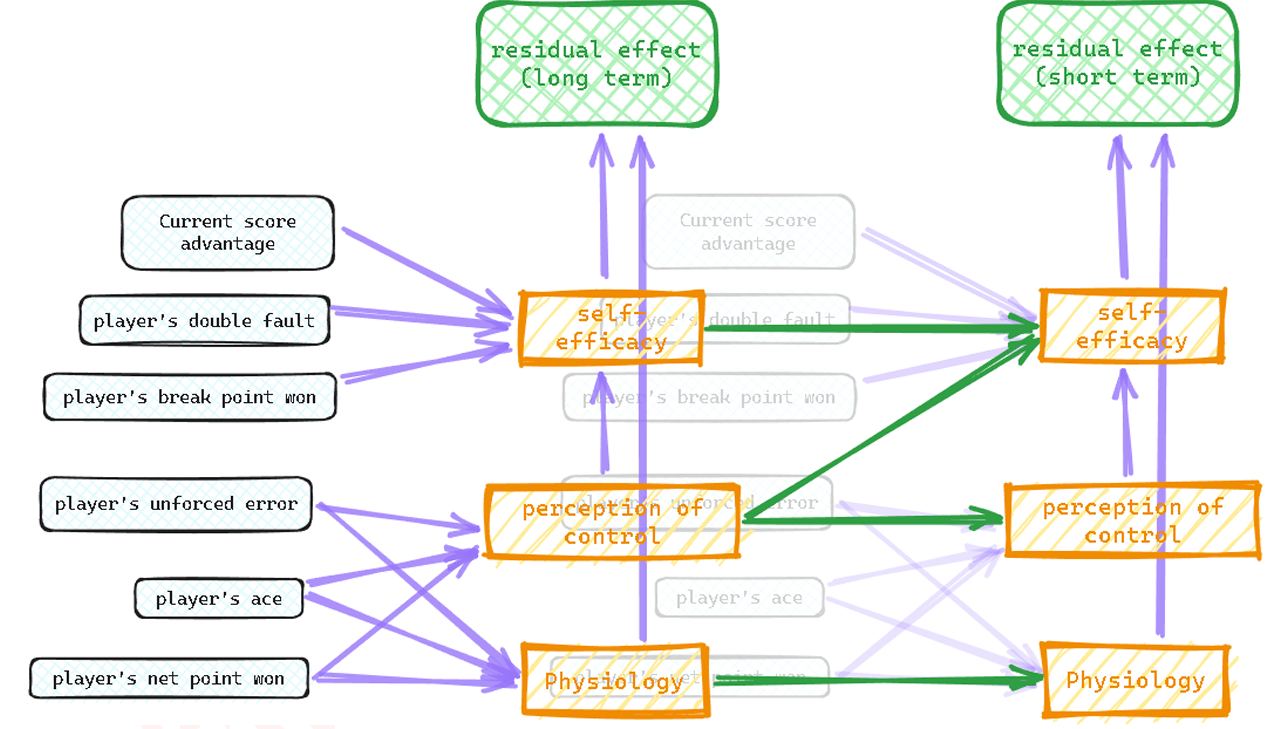
我们在这两层之间的隐藏变量上添加了绿色箭头，代表了心理和身体状态的连续性。
===== 第 17 页 =====
5.2.3 数据拟合
有效训练此模型的一个障碍是噪声。尽管我们已经考虑了原始实力差异和发球优势，但我们必须承认在某一得分点上得/失分的残余效应在很大程度上仍然是（并且应该仍然是）随机的。我们不让模型预测下一分中的状态，而是让它预测接下来 n 分中效应的总和。由于中心极限定理，这减少了噪声，从而使网络的训练成为可能。以同样的方式，所有观测变量，如球员的双误，都在某个时间区间内进行聚合。具体来说，假设当前点数索引是 tt，长期层的数据在 [t−40,t−10]区间内聚合，效应在 [t−10,t] 区间内聚合；而短期层的数据在 [t−10,t]区间内聚合，效应在 [t,t+10] 区间内聚合。我们仔细分离过去的比赛信息和未来的比赛结果，以确保我们的模型是完全预测性的。
下图描绘了卡洛斯·阿尔卡拉斯对阵德约科维奇的比赛中，从卡洛斯视角看，降噪后的残余效应变化。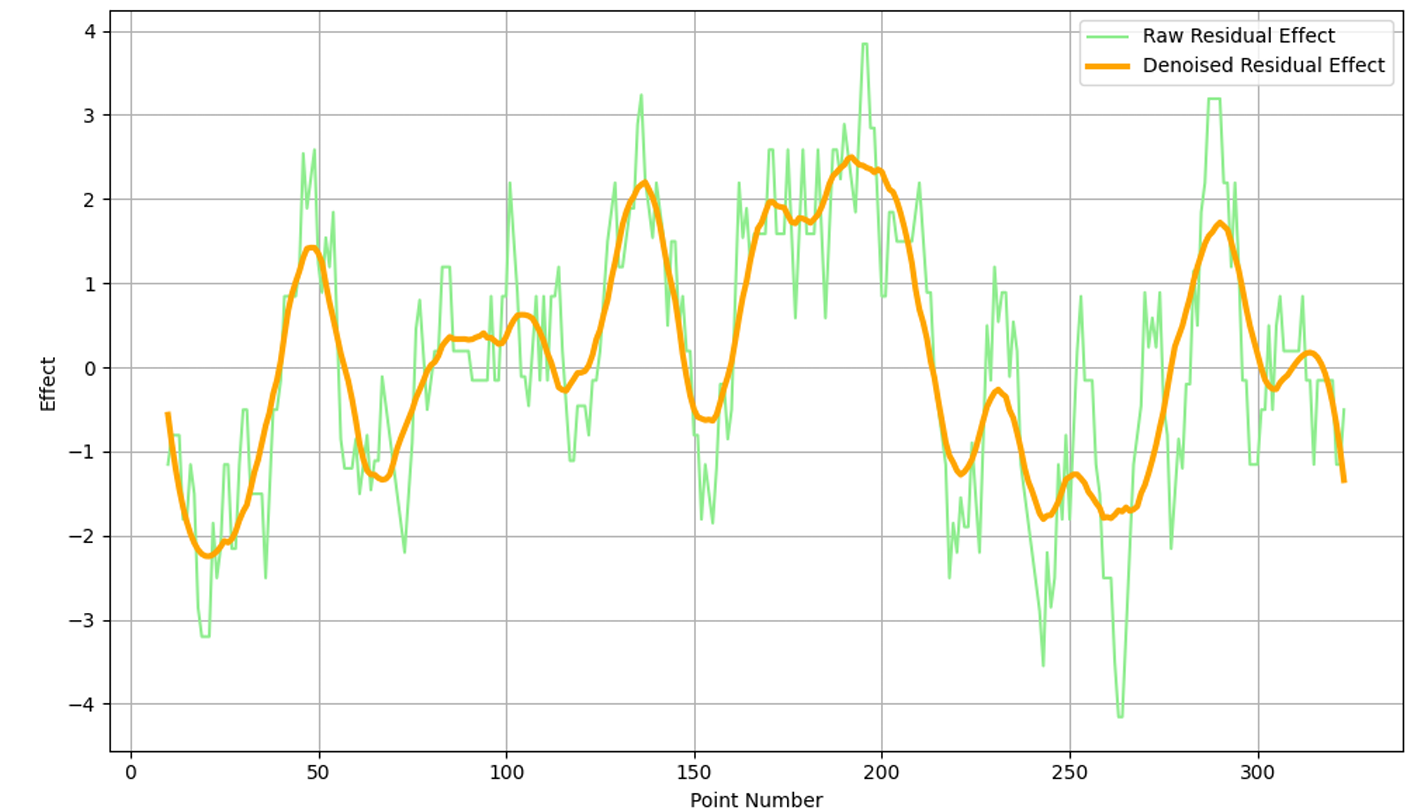
由于我们模型中存在潜在变量，我们利用期望最大化（EM）算法在 2023 年温网 31 场比赛的数据上训练网络。EM 算法用于在概率模型中寻找参数的最大似然估计，其中模型依赖于未观测到的潜在变量。
EM 算法包括两个步骤：期望步骤（E 步）和最大化步骤（M 步）。在 E 步中，算法根据模型的当前参数计算潜在变量的期望值。在 M 步中，它基于这些期望值最大化似然函数以更新参数。这个过程重复进行直到收敛。
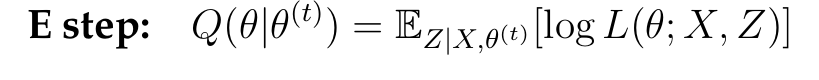
(13)
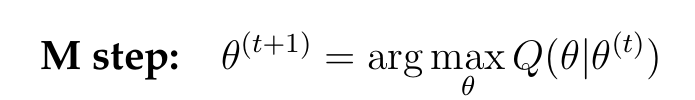(14)
在这些方程中，θ代表模型的参数，X 代表观测数据，包括输出——残余效应和输入——逐点数据，Z 代表潜在变量（我们模型中有 6 个潜在变量），L 是似然函数，Q是一个依赖于潜在变量期望值的函数。
在我们的第一次训练中，我们发现了这个数据集中的一个意外偏差：总体上，球员 1 比球员 2 具有更好的残余效应。因此，我们的模型预测的“球员 1 有更好的残余效应”与“球员 2 有更好的残余效应”的先验分布（即没有提供证据时）大约是 53% 对 47%。我们可以镜像数据集（即交换球员 1 和球员 2 的位置）但也会加倍训练成本。为了以更通用的方式解决这个问题，我们对 Q(θ∣θ(t))的表达式进行重新加权，如下：
(15)
其中 P(X) 是 X 发生的先验概率，考虑到它的一些特征——在我们的例子中，是残余效应优势。
为了有效地训练网络，我们首先需要对变量进行离散化。术语“残余效应 1(0)”和“残余效应 1(1)”分别指归因于对手和自己的势头。类似地，unfferr_1 的范围从 0 到 2，表示球员之间的相对非受迫性失误水平；‘0’ 意味着对手的非受迫性失误更多，‘1’ 表示水平相等，‘2’ 表明自己的非受迫性失误更多。至于潜在变量，如 self_efficacy_1，其值范围从 0 到 1，表示球员之间的相对自我效能感水平；‘0’ 意味着对手的自我效能感更高，‘1’ 表明自己的自我效能感更高。
为了衡量变量的重要性，我们计算了给定每个变量时的信息增益（或等价的，“熵减少”）。熵值提供了与不同变量对势头影响的预测相关的不确定性或不可预测性的度量。更大的信息增益表明更大的重要性。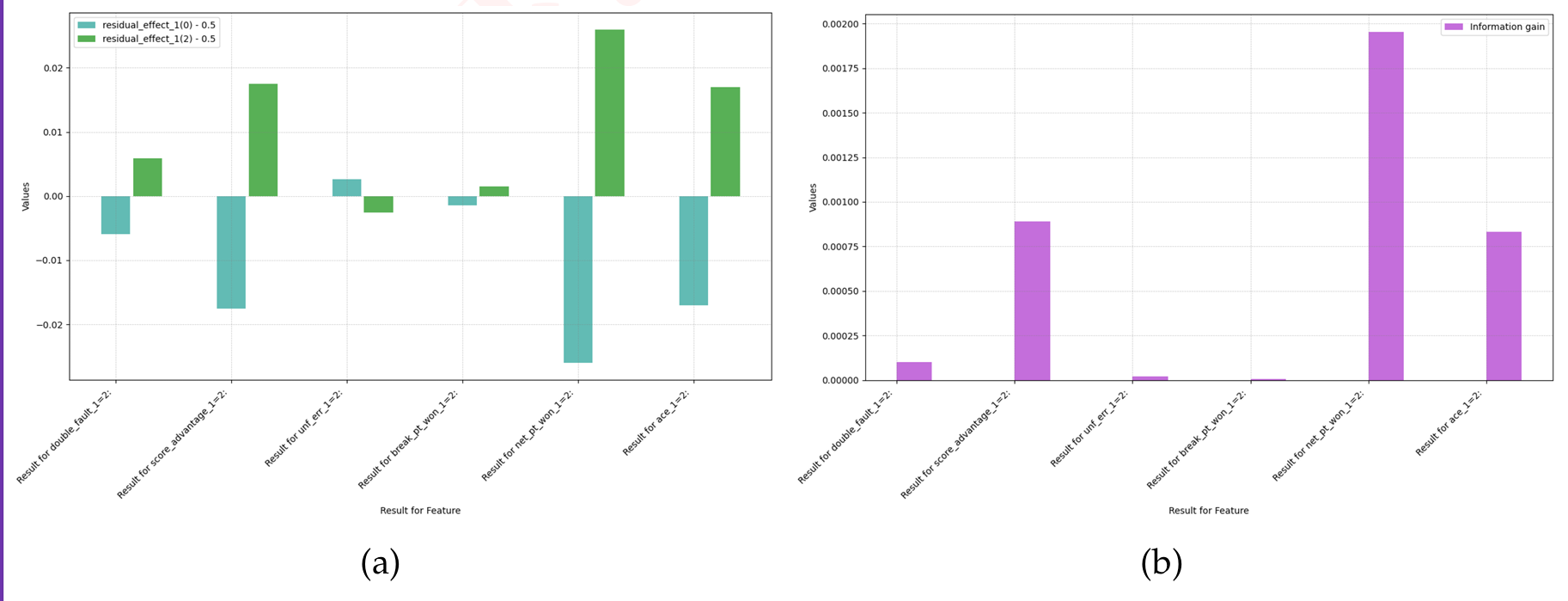
图 12：残余效应差异和熵
从图中可以看出，对势头最显著的正面影响来自球员的网前得分，其次是 Ace 球和保持领先优势。这些结果表明，积极主动和进攻性的打法对球员的势头有显著贡献。与此形成鲜明对比的是，非受迫性失误被证明会削弱势头，强调了在球场上保持心理优势时稳定性和失误管理的重要性。双误出人意料地似乎略微增加了势头。我们怀疑这是由于双误与进攻性发球之间的相关性。由于球员的进攻性未被识别为我们模型中的变量，因此真正的因果效应很难被学习。
为了进一步澄清双误后势头反直觉的增加，我们的研究深入探讨了发球的模式。发球方球员 1 和球员 2 的基线 Ace 球率 p1ace 和p2ace 分别为9.70% 和8.61%。有趣的是，对双误后的分析显示 Ace 球频率有所上升，在随后的十次发球中，球员 1 的 Ace 率 p1acenextdoublefault上升到 10.61%，p2acenextdoublefault上升到 9.59%。这表明模型学到了相关性捷径或数据偏差。
5.2.4 对比赛数据的推断
在推断过程中，所有观测变量，包括长期残余效应，都被输入模型。基于这些已知的证据，我们的贝叶斯网络可以确定输出和潜在变量的分布，并最终确定比赛中的势头（作为残余效应）。具体来说，给定网络的结构，我们可以使用网络中描述的条件依赖关系来描述这些变量分布之间的数学关系。有关计算细节，请参考 [(Ben,2007)][11]。
5.2.5 建议
基于我们贝叶斯网络的统计分析，我们为球员提出了以下策略，以潜在地改善他们的势头：
-
最小化非受迫性失误： 在回合中优先考虑稳定性，避免因可避免的失误而丢掉势头。
-
利用进攻性打法： 融合更多的网前打法并瞄准 Ace 球，以利用这些行动对势头的强烈积极影响。
-
策略性发球： 专注于发球的准确性和多样性，减少双误，尽管它们可能不会显著削弱势头，但保持发球局对比赛成功仍然至关重要。
-
心理韧性： 培养心理韧性以承受面对破发点的压力，因为克服它们对势头的贡献比预期的要小。
-
保持领先： 努力建立并保持领先，因为保持领先地位能培养积极的势头，并能对对手施加心理压力。
将这些策略融入训练和比赛中可以帮助球员利用和保持势头，这是竞技网球的一个关键方面。
6 问题 4：波动预测与模型泛化
我们首先在卡洛斯·阿尔卡拉斯对阵诺瓦克·德约科维奇的决赛中评估了我们的模型。结果，连同另外三场比赛的结果，呈现在后面的图表中。值得注意的是，我们的模型准确预测了残余效应的前几次起伏，但在第 230 到 280 分（对应第四盘）时失败了。在这个阶段，诺瓦克·德约科维奇意外地获得了显著优势。这可能是由于我们的模型未考虑的因素的影响。
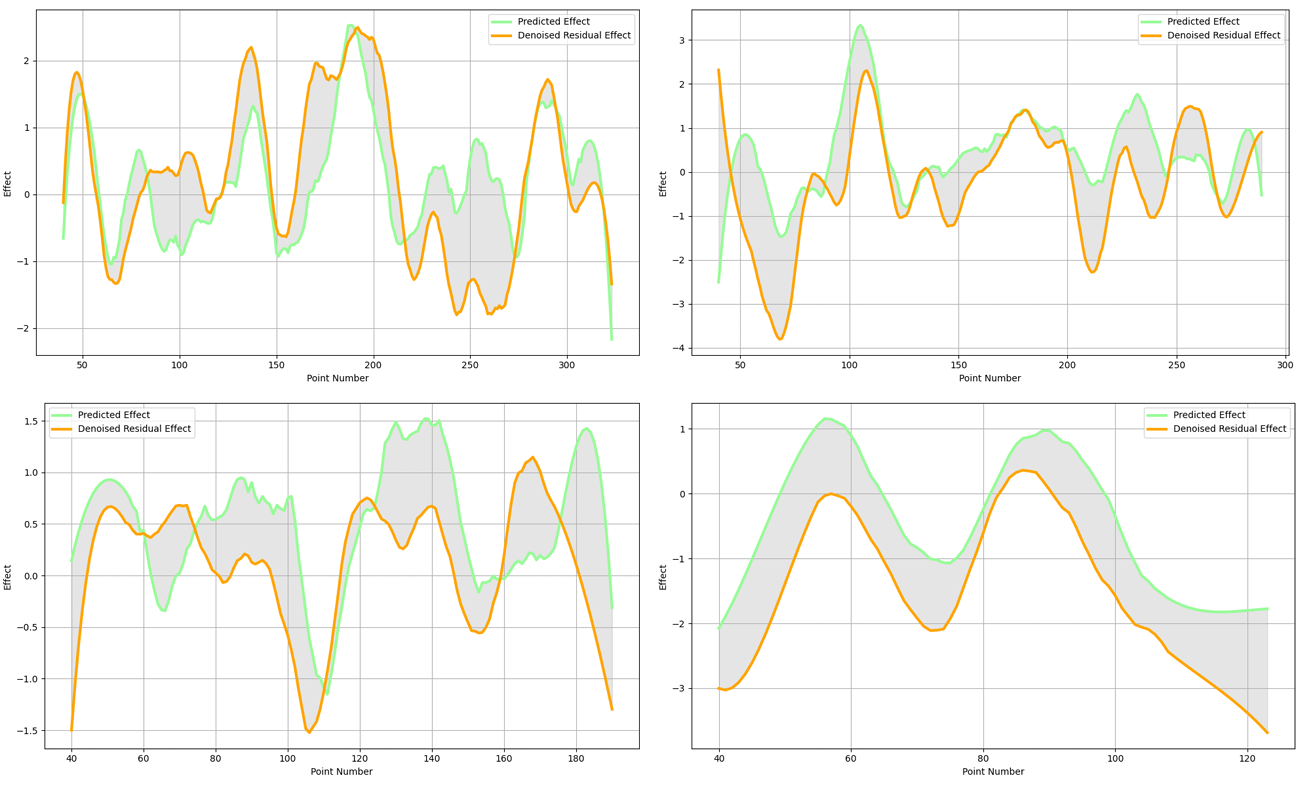
图 13：预测 vs 实际
一个可能显著影响网球比赛结果的因素是特定球员的个人打球风格，如场地偏好、伤病史。这些只能通过他们的历史表现来建模，无法通过我们当前的方法推断（即仅考虑球员排名）。基于数据的球员个人信息整合可能会进一步提升我们模型的性能。
此外，除了给定的温网数据集，我们还在一个女子单打网球比赛数据集上测试了我们的模型，该数据集来自 JeffSackmann 的 tennis_MatchChartingProject，名为 charting-w-points-2020s.csv [10]。
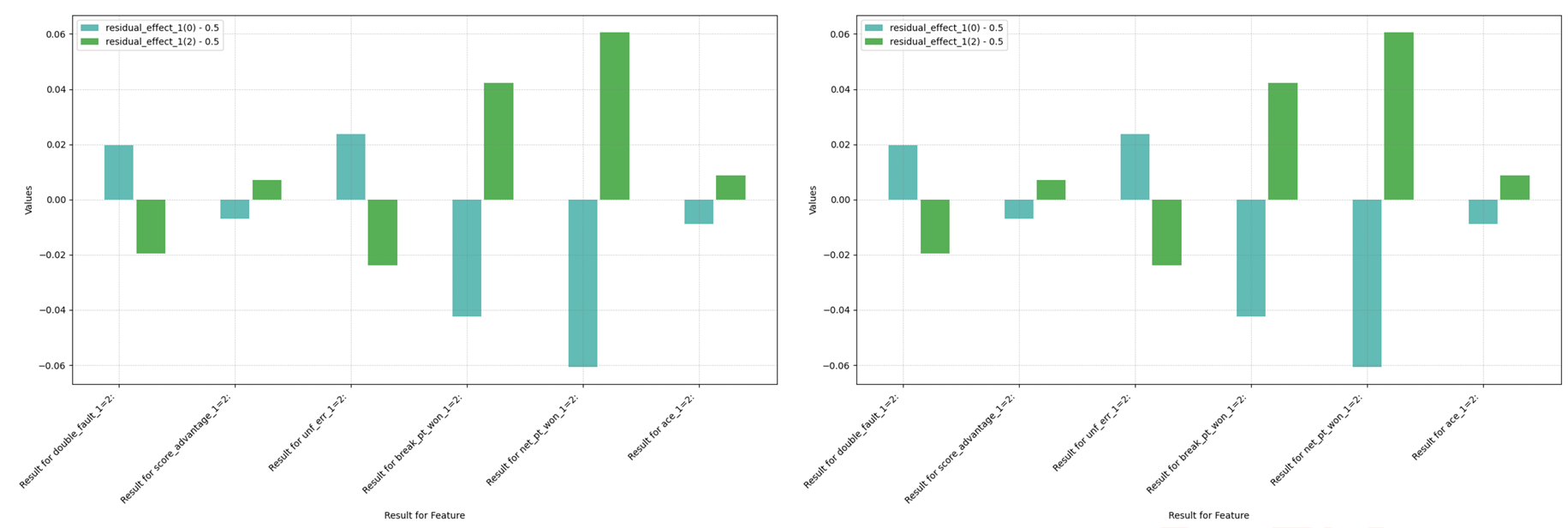
图 14：残余效应差异和熵（女子比赛）
与图 12 相比，一个显著的区别是 Ace 球的影响。在我们的数据集中，男性球员有 9.14%9.14% 的可能性发出 Ace 球，而女性球员只有 4.25%4.25%。此外，双误的发生现在明显有不利影响，因为它不再是试图发出 Ace 球的进攻性尝试的结果。
为了展示我们模型框架的适应性，我们进一步将其泛化为更抽象和全面的形式，如下图所示。这个框架可以被实例化为能够处理各种体育比赛（如乒乓球、篮球、足球...）的模型。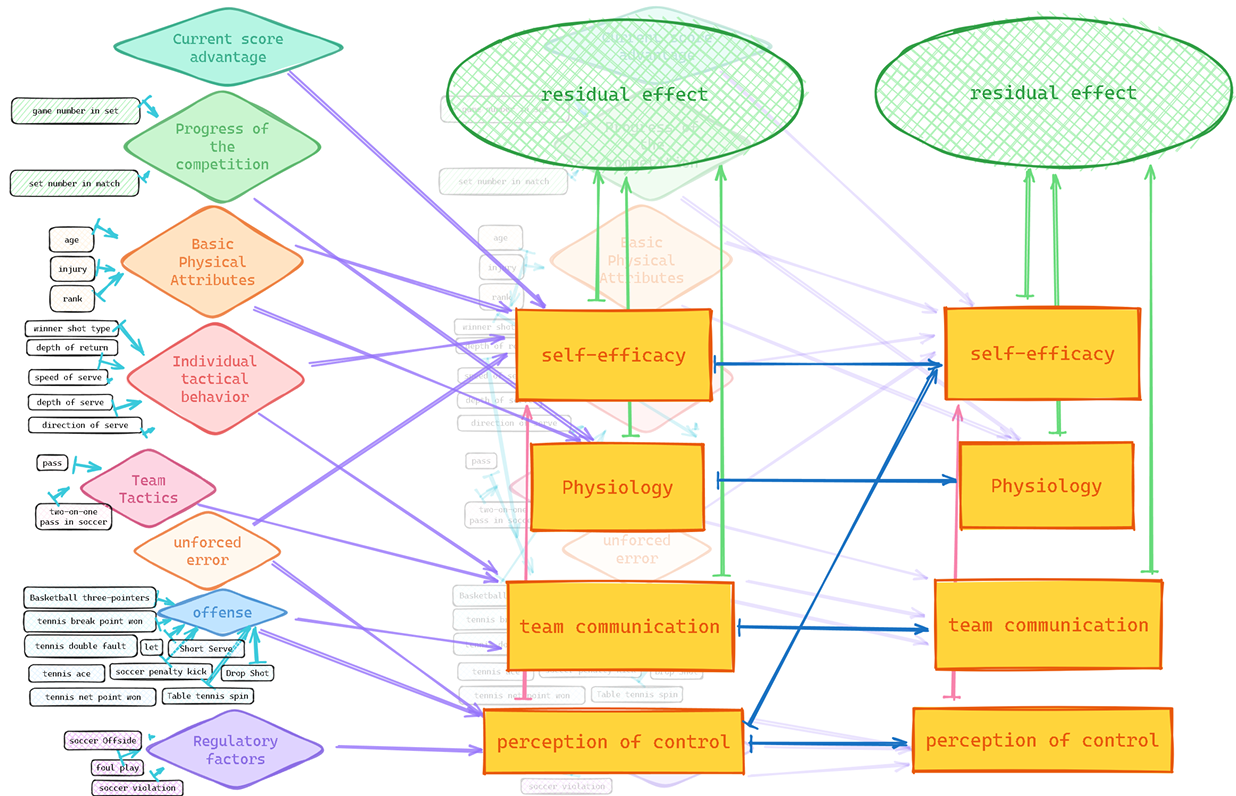
===== 第 22 页 =====
7 模型分析
7.1 优点与缺点
优点：
-
通过双层结构捕捉短期和长期势头效应。这允许模型解释来自近期比赛事件的势头转变以及长期的心理因素。
-
纳入了潜在变量，如生理状态、控制感和自我效能感，这些变量无法直接观测但在势头上起着重要作用。这为影响势头的因素提供了更全面的表示。
-
使用了先进的机器学习技术，如期望最大化，来处理潜在变量并使模型能够在真实比赛数据上训练。这使得模型具有实际应用性。
-
在数据集中的不同球员和比赛上实现了良好的泛化，展示了鲁棒性。
-
提供了关于不同因素（如非受迫性失误、进攻性打法、破发点等）如何影响势头的可解释见解。
缺点：
-
由于无法获取球员心理状态的实际测量数据，难以完全验证潜在变量表示及其动态的准确性。
-
需要将数据在区间上聚合以减少训练噪声，损失了一些粒度。
-
没有考虑对手的适应性策略及其对势头的影响。假设了球员行为的独立性。
7.2 敏感性分析
为了评估我们提出模型的鲁棒性，我们在两个方面进行了敏感性分析。1. 修改模型的预测区间。2. 通过从原始数据集中随机采样 70%70% 和 50%50% 来改变训练数据，分别对应 22 场和 16 场比赛。
下图显示了观测变量信息增益的变化。左图的变化表明，更长的预测区间迫使模型优先考虑可能持续时间更长的效应，例如“分数优势”。相反，短期事件如“网前得分”、“Ace 球”获得的权重较小。在右图中，在 50%50% 数据上训练的模型出现了显著变化，可能是由于比赛分布的改变。另一方面，在 70%70% 数据上训练的模型保持稳定，表明达到了数据充分性的阈值。
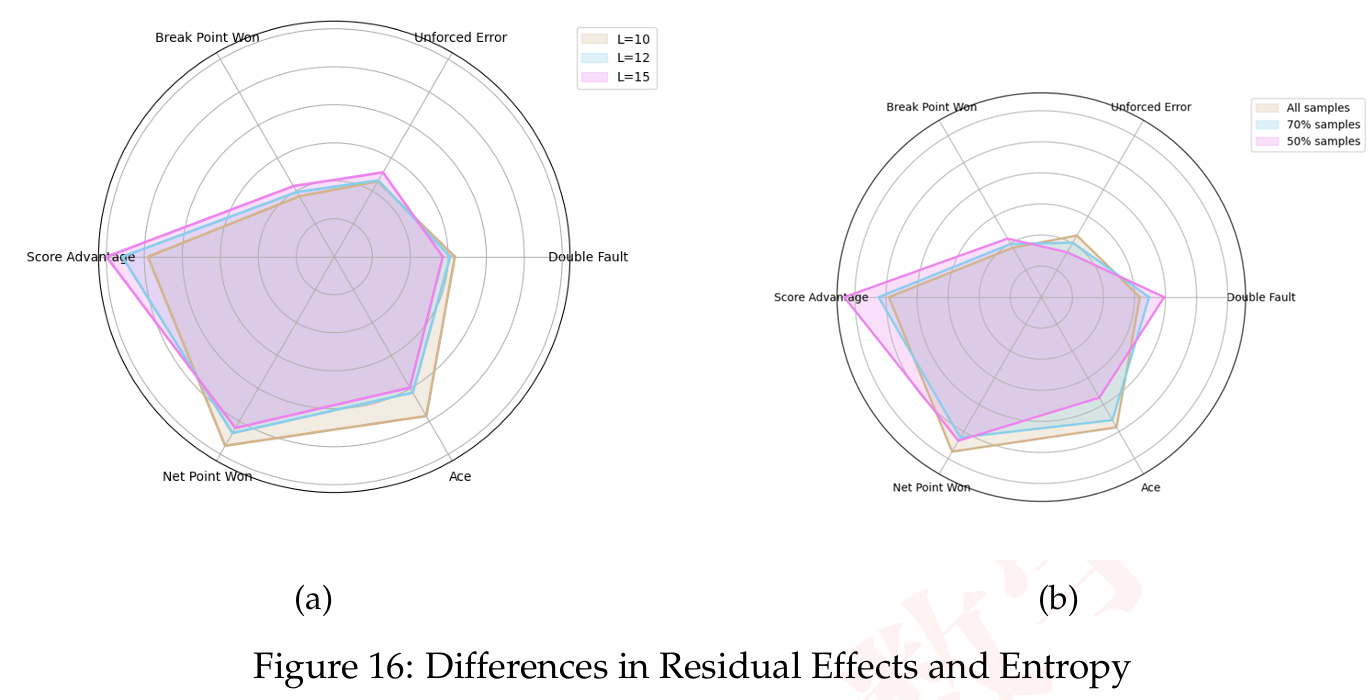
图 16：残余效应差异和熵（敏感性分析）
7.3 结论
在本文中，我们通过一个两步过程建立了我们的势头预测器。首先，我们开发了一个旨在恢复比赛“理想”状态的朴素二项模型。随后，其预测的残差被用作我们的势头预测器——双时间贝叶斯网络的标签。这个模型框架被证明具有高度泛化性和鲁棒性，使我们能够揭示可观测体育比赛背后的潜在系统。
8 备忘录
致： 网球教练
发件人： 队伍 #2401298
主题： 利用网球中的势头——教练见解与策略
日期： 2024 年 2 月 6 日
尊敬的教练们，
我们非常高兴能与您分享来自我们双时间贝叶斯网络模型的建议，旨在通过网球中“势头”这一微妙概念来提升球员表现。在竞争激烈的网球世界中，“势头”的概念常被引为改变比赛的关键，可能决定比赛关键时刻的走向。这种难以捉摸的力量被认为可以塑造比赛结果。我们的研究剖析了这一现象，旨在将抽象的现象转化为可系统应用的具体策略。
图 17：网球中的势头
“势头”不是一个孤立的概念，它代表了网球比赛复杂潜在状态的存在，超越了仅通过计算分数所能捕捉的内容。我们的研究分析了网球比赛中势头的复杂动态。我们利用统计模型和双时间贝叶斯网络来量化和预测心理及生理因素对比赛表现的影响。我们的分析表明，虽然每个得分的结果在统计上可能在一定程度上显得独立，但我们开发的贝叶斯网络讲述了一个更丰富的故事。它揭示了自我效能感、策略和生理反应这些交织在一起形成势头结构的隐藏线索。
为了使球员能够利用势头的积极方面同时减轻其压力，我们建议遵循以下策略支点：
-
稳定性是关键： 鼓励球员最小化非受迫性失误；我们的发现将稳定的表现与保持势头联系起来。
-
进攻性有回报： 建议球员通过网前打法和发球来确立主导地位，以建立积极的势头。
-
明智发球： 强调多变和准确的发球技术，在不冒双误风险的情况下保持势头。
-
培养韧性： 培养球员的心理韧性，这对于应对破发点的压力和比赛中的潮流转变至关重要。
-
领先以成功： 争取早期领先；我们的模型表明这会给对手施加心理压力，增强领先球员的势头。
我们相信这份备忘录为您提供了一个清晰且可操作的策略，以利用势头概念为您带来优势。实施这些建议可以培养竞争优势，这对于在现代快节奏的网球比赛中取胜至关重要。
期待看到这些策略在您球员的增强表现中得以体现。
此致，敬礼，
队伍 #2401298
===== 第 25 页 =====
参考文献
[1] Taylor, J., & Demick, A. (1994). A multidimensional model of momentum in sports. Journal of Applied Sport Psychology, 6(1), 51-70.
[2] Klaassen, F. J., & Magnus, J. R. (2001). Are points in tennis independent and identically distributed? Evidence from a dynamic binary panel data model. Journal of the American Statistical Association, 96(454), 500-509.
[3] Motoi, S., Misu, T., Nakada, Y., Yazaki, T., Kobayashi, G., Matsumoto, T., & Yagi, N. (2012). Bayesian event detection for sport games with hidden Markov model. Pattern Analysis and Applications, 15, 59-72.
[4] Sun, Y. (2004). Detecting the hot hand: An alternative model. In Proceedings of the Annual Meeting of the Cognitive Science Society (Vol. 26, No. 26).
[5] Klaassen, F. J., & Magnus, J. R. (2003). Forecasting the winner of a tennis match. European Journal of Operational Research, 148(2), 257-267.
[6] Ge, X., & Lin, A. (2021). Dynamic causality analysis using overlapped sliding windows based on the extended convergent cross-mapping. Nonlinear Dynamics, 104, 1753-1765.
[7] Morber, J. R. (2008). One-dimensional nanowires: Understanding growth and properties as steps toward biomedical and electrical application. Georgia Institute of Technology.
[8] Madhavan, V. (2016). Predicting NBA game outcomes with hidden Markov models. Berkeley University.
[9] Raab, M., Gula, B., & Gigerenzer, G. (2012). The hot hand exists in volleyball and is used for allocation decisions. Journal of Experimental Psychology: Applied, 18(1), 81.
[10] https://github.com/JeffSackmann/tennis_MatchChartingProject.
[11] Ben Gal I (2007). "Bayesian Networks" (PDF). In Ruggeri F, Kennett RS, Faltin FW (eds.). Support-Page. Encyclopedia of Statistics in Quality and Reliability. John Wiley & Sons. doi:10.1002/9780470061572.eqr089. ISBN 978-0-470-01861-3. Archived from the original (PDF) on 2016-11-23. Retrieved 2007-08-27.
