如何用近似算法解决NP难问题：Algorithms39完整指南
如何用近似算法解决NP难问题：Algorithms39完整指南
【免费下载链接】Algorithms A collection of algorithms and data structures 
项目地址: https://gitcode.com/gh_mirrors/algorithms39/Algorithms
在计算机科学领域，近似算法是解决NP难问题的关键工具，能够在多项式时间内找到接近最优解的方案。Algorithms39项目提供了丰富的算法实现，特别在旅行商问题、斯坦纳树和背包问题等领域展现了强大的实用价值。🎯
什么是NP难问题和近似算法
NP难问题是指那些在多项式时间内无法找到精确最优解的问题，但它们的最优解可以在多项式时间内被验证。近似算法通过在合理的时间内提供接近最优解的方案，为这些看似"无解"的问题找到了突破口。
核心概念解析
- NP难问题：旅行商问题、斯坦纳树问题、0/1背包问题
- 近似比：算法解与最优解之间的比值保证
- 多项式时间：算法运行时间与输入规模成多项式关系
二叉搜索树作为高效数据结构支撑近似算法的实现
Algorithms39中的关键近似算法实现
旅行商问题（TSP）近似解法
在src/main/java/com/williamfiset/algorithms/graphtheory/TspDynamicProgrammingIterative.java中，项目实现了从O(n!)到O(n²·2ⁿ)的时间复杂度优化，这在处理中等规模问题时具有重要价值。
算法特点：
- 动态规划方法大幅提升效率
- 适用于城市数量不超过32的实际场景
- 提供接近最优的路径规划方案
斯坦纳树问题解决方案
src/main/java/com/williamfiset/algorithms/graphtheory/SteinerTree.java展示了如何找到连接给定终端节点的最小成本树结构。
0/1背包问题近似算法
项目中的src/main/java/com/williamfiset/algorithms/dp/Knapsack_01.java实现了经典的动态规划解法，时间复杂度为O(nW)，在大多数实际应用中表现优异。
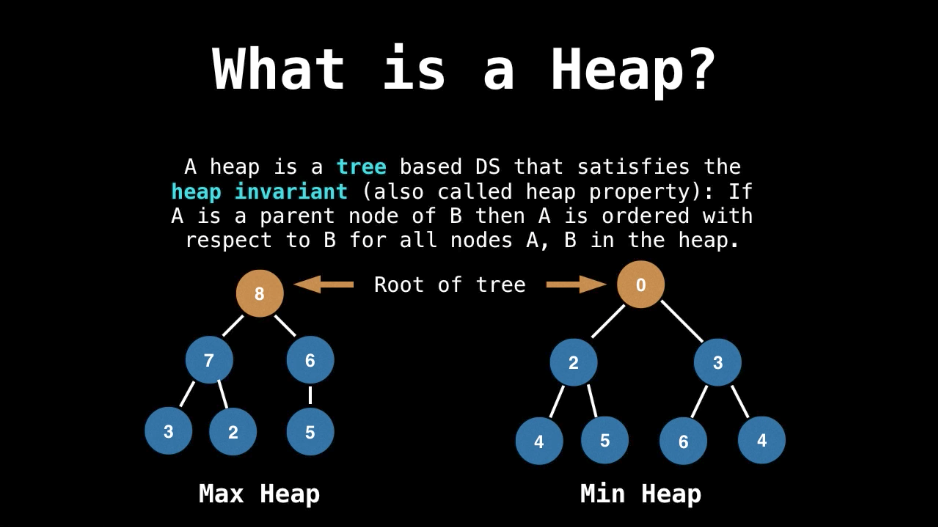优先队列在贪心近似算法中发挥重要作用
近似算法的实际应用场景
网络优化与路由规划
- 电信网络中的基站部署
- 物流配送路径优化
- 数据中心网络设计
资源分配与调度
- 云计算资源分配
- 生产调度优化
- 投资组合管理
算法性能分析与选择指南
时间复杂度对比
| 算法类型 | 时间复杂度 | 适用场景 |
|---|---|---|
| 精确算法 | 指数级 | 小规模问题 |
| 近似算法 | 多项式级 | 中大规模问题 |
实际应用建议
- 问题规模评估：根据输入规模选择合适的算法
- 精度要求分析：确定可接受的近似程度
- 计算资源考量：平衡时间与空间复杂度
快速上手与代码示例
要运行项目中的近似算法实现，可以使用Bazel构建工具：
bazel run //src/main/java/com/williamfiset/algorithms/graphtheory:SteinerTree
核心模块路径速查
- 动态规划模块：
src/main/java/com/williamfiset/algorithms/dp/ - 图论算法：
src/main/java/com/williamfiset/algorithms/graphtheory/ - 数据结构支持：
src/main/java/com/williamfiset/algorithms/datastructures/
总结与展望
近似算法为解决NP难问题提供了实用的工程解决方案，Algorithms39项目通过精心实现的算法库，为开发者和研究人员提供了强大的工具支持。🚀
通过合理选择和应用这些算法，我们能够在可接受的时间内获得满足实际需求的优质解，这在当今大数据和复杂系统时代具有极其重要的现实意义。
【免费下载链接】Algorithms A collection of algorithms and data structures 项目地址: https://gitcode.com/gh_mirrors/algorithms39/Algorithms
