堆排序（C语言）

2026-02-01 09:26:54 栏目：最新资讯 8 阅读

文章目录

堆排序
- 堆的概念
- 小顶堆操作
- - 插入元素：
  - - 顶向下的upAdjust
    - 自底向上的downAdjust
  - 删除元素，从堆顶来提取
- 大顶堆实现

堆排序

堆的概念

堆（Heap）是一类基于完全二叉树的特殊数据结构。

分成两种类型：

1、大顶堆（MaxHeap）：
在大顶堆中，根节点的值必须大于他的孩子节点的值，对于二叉树中所有子树都满足此规律；

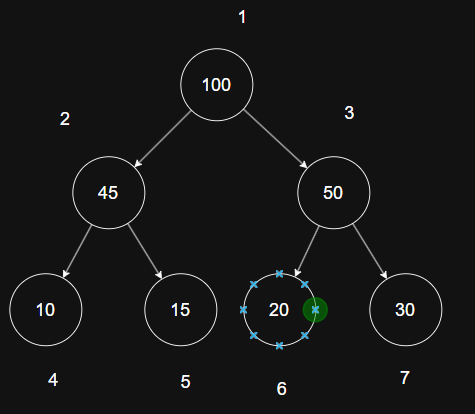
2、小顶堆（MinHeap)：
在小顶堆中，根节点的值必须小于他的孩子节点的值，对于二叉树中所有子树都满足此规律；

最小堆初始数：9,3,7,6,5,1,10,2
完全二叉树，顺序存储，从下标为1节点上进行数据存储，任意节点i的关系[i/2,i,2i,2i+1][父节点，当前节点，左孩子，右孩子]

注意不一定是二叉排序树

小顶堆操作

插入元素：

upAdjust和downAdjust是两种完全不同的建堆/调整方法。

顶向下的upAdjust

（逐个插入元素，每次插入后向上调整）。

1.在最后一个位置，插入新元素
2.上浮找到这个新元素的父节点，如果父节点大了，那么就交换父子
3.继续将交换的父节点值当做待确定值，再和他的父节点比较
4.不断循环，直到达到根节点或者满足堆性质

// upAdjust: 从节点i向上调整，直到根节点
void upAdjust(int* a, int i) {
    while(now > 1) {        // 向上遍历
        next = now / 2;     // 找父节点
        if(a[now] > a[next]) {  // 与父节点比较
            swap(...);
            now = next;     // 向上移动
        } else break;
    }
}

自底向上的downAdjust

（从n/2到1向下调整）

为什么从 n/2 开始？

下标大于 n/2 的节点都是叶子节点,叶子节点没有子节点，自然满足堆性质,只需要调整非叶子节点
假设 n=10：
- 叶子节点：下标6-10（5个节点）
- 非叶子节点：下标1-5（5个节点）
我们只调用 downAdjust 5次（而不是10次），因为：
- 下标6-10的节点是叶子，已经是"堆"
- 不需要对它们进行任何操作

为什么递减到 1？

自底向上构建，确保调整父节点时，其子树已经是堆

当我们对一个节点进行调整时，我们假设它的左右子树都已经是堆（满足堆的性质）。我们是按照从后往前的顺序调整的，当我们调整一个节点时，它的左右子节点作为更底层的子树，已经被调整过了（因为下标更大，而我们是从后往前调整）

先让底层子树成为堆，再逐步向上合并
关键：我们只需要比较当前节点和它的直接孩子，因为：
- 子树已经是堆
- 如果当前节点 ≥ 直接孩子，那么它也一定 ≥ 所有后代（因为孩子是子树的根)

	//向下调整进行建堆
	for(int i=n/2;i>=1;i--)//枚举子树根结点的下标
	{
		downAdjust(a,i,n);
	}

// downAdjust: 从节点i向下调整，直到叶子
/*int *a：数组/堆的指针
int i：需要向下调整的起始节点下标
int n：堆的有效范围边界（最后一个元素的下标）*/
void downAdjust(int *a, int i, int n) {
    while(2 * now <= n) {   // 向下遍历
        next = 2 * now;     // 找左孩子
        if(next+1 <= n && a[next+1] > a[next]) {
            next++;         // 找更大的孩子
        }
        if(a[now] < a[next]) {  // 与孩子比较
            swap(...);
            now = next;     // 向下移动
        } else break;
    }
}

删除元素，从堆顶来提取

1.完全二叉树，删除一个元素，只能删除最后一个元素
2.删除堆顶，取出堆顶的元素值，用最后一个元素来替代根
3.下沉，有左孩子的话不是最后一个，如果有右孩子，左孩子一定有（不是最后一个元素，二叉树性质），比较左孩子和右孩子谁最小

最后一个非叶子节点的索引是：⌊n/2⌋

当 n 为偶数时，这个节点只有一个左孩子。
当 n 为奇数时，这个节点有两个孩子。

4.最小的进行交换

初始数组和树形表示

数组索引: 1  2  3  4  5  6
元素值:   5  3  8  1  4  6

树形结构:
        5(1)
       /     
     3(2)     8(3)
    /        /
  1(4)  4(5) 6(6)

循环过程：for(int i = n/2; i >= 1; i--)

第1轮：i = 3 (n/2 = 6/2 = 3)

调整节点 3（值=8）及其子树

调整前：
        5(1)
       /     
     3(2)     8(3) ← 调整这个节点
    /        /
  1(4)  4(5) 6(6)

检查节点3：
- 左孩子：下标6，值=6
- 右孩子：下标7 > n，不存在
- 比较：8 > 6，不需要交换

调整后（没有变化）：
        5(1)
       /     
     3(2)     8(3)
    /        /
  1(4)  4(5) 6(6)

第2轮：i = 2 (值=3)

调整节点 2（值=3）及其子树

调整前：
        5(1)
       /     
     3(2) ← 调整这个节点  8(3)
    /        /
  1(4)  4(5) 6(6)

检查节点2：
- 左孩子：下标4，值=1
- 右孩子：下标5，值=4
- 最大的孩子：右孩子(4) > 左孩子(1)，所以最大孩子是下标5，值=4
- 比较：3 < 4，需要交换

交换节点2(3)和节点5(4)：
        5(1)
       /     
     4(2)     8(3)
    /        /
  1(4)  3(5) 6(6)

检查节点5(现在是3)：
- 左孩子：下标10 > n，不存在
- 右孩子：下标11 > n，不存在
- 停止调整

第3轮：i = 1 (值=5)

调整根节点 1（值=5）及其整棵树

调整前：
        5(1) ← 调整这个节点
       /     
     4(2)     8(3)
    /        /
  1(4)  3(5) 6(6)

检查节点1：
- 左孩子：下标2，值=4
- 右孩子：下标3，值=8
- 最大的孩子：右孩子(8) > 左孩子(4)，所以最大孩子是下标3，值=8
- 比较：5 < 8，需要交换

交换节点1(5)和节点3(8)：
        8(1)
       /     
     4(2)     5(3)
    /        /
  1(4)  3(5) 6(6)

检查节点3(现在是5)：
- 左孩子：下标6，值=6
- 右孩子：下标7 > n，不存在
- 最大的孩子：左孩子(6)
- 比较：5 < 6，需要交换

交换节点3(5)和节点6(6)：
        8(1)
       /     
     4(2)     6(3)
    /        /
  1(4)  3(5) 5(6)

检查节点6(现在是5)：
- 左孩子：下标12 > n，不存在
- 停止调整

最终建堆结果

数组状态: [8, 4, 6, 1, 3, 5]
树形结构:
        8(1)
       /     
     4(2)     6(3)
    /        /
  1(4)  3(5) 5(6)

这是一个大顶堆！
- 节点1(8) ≥ 子节点2(4)和3(6)
- 节点2(4) ≥ 子节点4(1)和5(3)
- 节点3(6) ≥ 子节点6(5)

大顶堆实现

堆排序分为两个阶段：

建堆阶段：将无序数组构建成一个大顶堆
排序阶段：重复提取最大值并放到数组末尾，逐步缩小堆的范围

#include

static swapa(int* a, int* b) {
	int t = *a;
	*a = *b;
	*b = t;
}
//大顶堆

//当前i 父节点i/2 左孩子2*i 右孩子2*i+1
//传进来第几个和树数组
void upAdjust(int *a, int i) {
	int cur = i;//当前节点
	int parent;//双亲节点

	//一直上浮直到根
	while (cur > 1) {
		parent = cur / 2;
		//比较双亲节点
		if (a[cur] > a[parent]) {
			swapa(&a[cur], &a[parent]);
			cur = parent;
		}
		else {
			break;//就是已经上浮不了
		}
	}
}

//下滤
/*a：要操作的数组
1：总是从根节点开始，因为每次交换后根节点可能不符合堆性质
k：当前堆的边界，确保只调整未排序的部分*/
void downAdjust(int* a, int i, int boundary) {
	int cur = i;//下 节点
	//小于等于 为非叶子节点
	while(cur<=boundary/2)
	{
		int lchild = 2 * i;
		int rchid = 2 * i + 1;
		int choose=lchild;//肯定有左孩子
		//有右孩子前提下比较孩子的大小 选择大的交换 越上越大
		if (a[lchild] < a[rchid]&&rchid<=boundary) {
			choose = rchid;
		}

		if (a[choose] > a[cur]) {
			swapa(&a[choose], &a[cur]);
			cur = choose;
		}
		else {
			break;//不用下了
		}

	}
}

int main() {
	int n;
	int a[105];
	scanf("%d", &n);
	for (int i = 1; i <= n; i++)
	{
		scanf("%d", &a[i]);
		//upAdjust(a, i);//上浮建堆  效率低
	}
	//1.建堆
	//底向上构建，确保调整父节点时，其子树已经是堆
//先让底层子树成为堆，再逐步向上合并
	//向下调整进行建堆
	for (int i = n/2; i >= 1; i--)
	{
		//下标大于 n/2 的节点都是叶子节点,叶子节点没有子节点，自然满足堆性质,只需要调整非叶子节点
		downAdjust(a, i, n);
	}


	//2.排序
	/*1.完全二叉树，删除一个元素，
	只能删除最后一个元素(度为0)
	2.删除堆顶，取出堆顶的元素值，
	用最后一个元素来替代根
	3. 下沉 ，有左孩子的话不是最后一个，
	 如果有右孩子，左孩子一定有  （不是最后一个元素，二叉树性质），
	比较左孩子和右孩子谁最小*/

	int k = n;//堆的边界 初始为n
	//[1,k]		[k+1,n]
	//无序区		有序区
	//通过下而上的“上浮”把无序区中最大的放在最后
	for (int i = 1; i <= n-1; i++)//排序趟数
	{
		
		swapa(&a[1], &a[k]);
		k--;
		/*a：要操作的数组
1：总是从根节点开始，因为每次交换后根节点可能不符合堆性质
k：当前堆的边界，确保只调整未排序的部分*/
		downAdjust(a, 1, k);//堆里面下浮
	}

	for (int i = 1; i <= n; i++)
	{
		printf("%d ", a[i]);
	}
	 
	return 0;
}