P1028 数的运算(递归/线性dp) (洛谷 NOIP)
数的计算
题目描述
输入一个自然数 n (n≤1000)n (n≤1000)，我们对此自然数按照如下方法进行处理:
-
不作任何处理;
-
在它的左边加上一个自然数,但该自然数不能超过原数的一半;
-
继续按照规则2添加，但是添加的数不能超过上一次添加数的一半，直到不能添加为止。
问总共可以产生多少个数。
输入描述
输入一个正整数 nn。
输出描述
输出一个整数，表示答案。
输入输出样例
示例 1
输入
6
输出
6
运行限制
- 最大运行时间：1s
- 最大运行内存: 128M
AC代码
递归
老实说，这道题目的意思不算好理解，看了好几遍才明白他想干什么，第一遍用递归写完后，计算的结果就是少了一个，debug半天后来才知道这里所说的产生数需要加上输入的n，有关题目和递归解法的解析这里有大佬的解法，她说的非常详细！很推荐大家去看看
递推（数正方形、数的计算）（2019蓝桥杯国赛）（好题持续更新）-CSDN博客
https://blog.csdn.net/2401_89133765/article/details/157438806?spm=1001.2014.3001.5501
线性dp
其实不难发现，本题存在明显的重叠子问题特征。不妨设当原数为 i 时，一共可产生 f(i) 个合法的数。以 n=6 为例，求解 f(6) 需要依赖子状态 f(1), f(2), f(3)。然而在求解 f(2) 和 f(3) 的过程中，会再次发起对 f(1) 的递归调用，因此可以得到状态转移方程 f(i) = f(i) + f(1) + f(2) + ··· + f(i/2)
线性dp的再次优化
上述的线性dp已经通过递推处理了重复计算的次数，但是时间复杂度还是O(n²)，再仔细观察题目给的例子，惊喜的发现依然有重复情况可以进行优化！
我们列出前几个数字的答案：
-
i为奇数1 f(1) = 1
-
i为偶数2 f(2) = 1 + f(1) = 2
-
i为奇数3 f(3) = 1 + f(1) = 2
-
i为偶数4 f(4) = 1 + f(1) + f(2) = 4
-
i为奇数5 f(5) = 1 + f(1) + f(2) = 4
-
i为偶数6 f(6) = 1 + f(1) + f(2) + f(3) = 6
发现了吗？
-
奇数项等于前一项：当 i 是奇数时，i/2 和 (i-1)/2 的结果是一样的（向下取整），所以 f(i) = f(i-1)。
-
偶数项多了一项：当 i 是偶数时，f(i) = f(i-1) + f(i/2)。
因此我们可以分奇偶讨论，这样就将时间复杂度优化到O(n)啦，下面是最终代码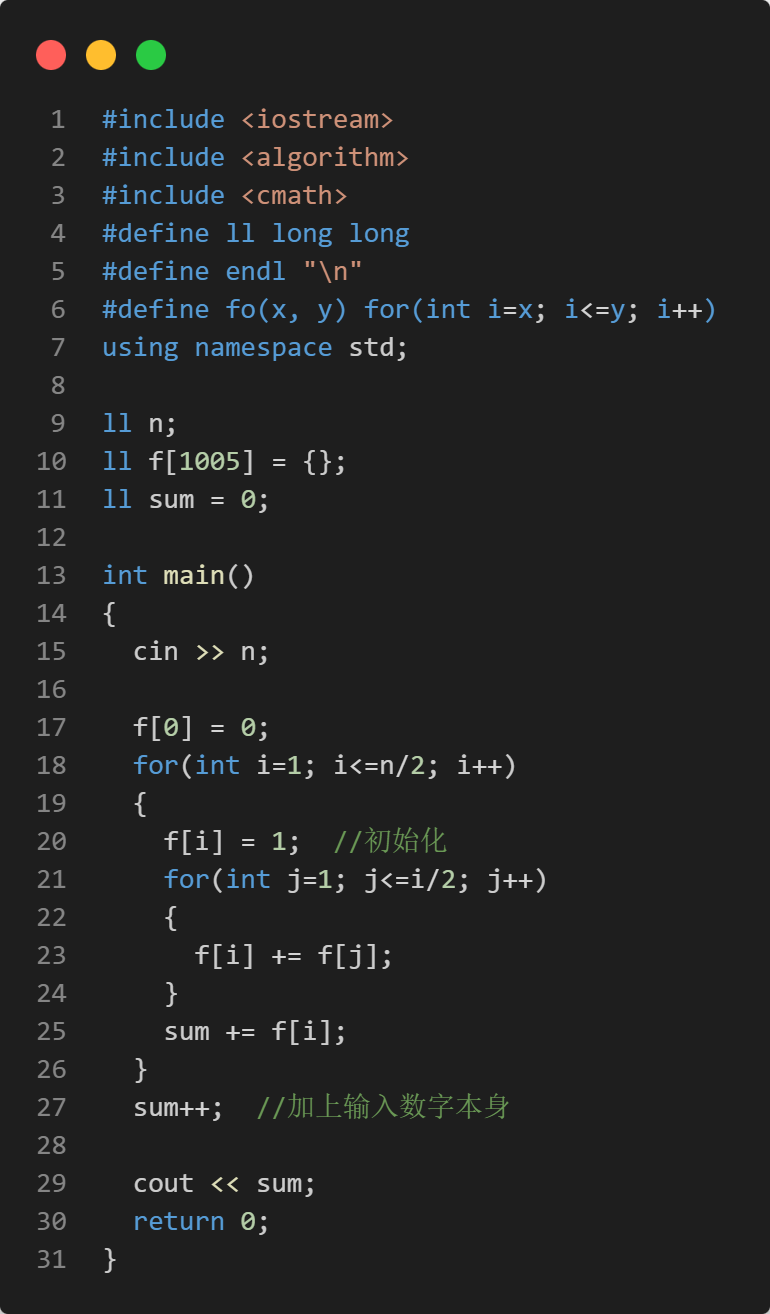
本题的题解就到这里啦，撒花~~✌
