2024 SNCPC 单挑记录
补题链接:https://codeforces.com/gym/105257
solved 7 out of 13.
题解按开题顺序排列。
A
题目大意
在 Linux 系统中,每个文件都有与之相关的权限,权限被分为读、写与执行三种权限(rwx)。
在本题中,chmod 模式串由若干 000 到 999 之间的十进制数组成,其二进制形式表示是否有对应权限。
例如数字 777 的二进制形式为 111111111,那么表示权限字符串为 rwx;数字 555 的二进制形式为 101101101,对应的权限为 r-x。
给出一个合法 chmod 模式串,输出对应的权限字符串。
输入包含 ttt 组测试数据。
其中
- 1≤t≤1001le tle 1001≤t≤100
思路
计算 chmod 串中每一位的二进制形式,然后按照题意输出就行。
Code
#include F
题目大意
给定长度为 nnn 的数组 {a}{a}{a},找出两个可以重复的整数 iii 和 jjj,最大化 ai&aja_i&a_jai&aj 的结果。
输入包含 ttt 组测试数据。
其中
- 1≤t≤2×1051le tle 2 imes 10^51≤t≤2×105
- 1≤n≤2×1051le nle 2 imes 10^51≤n≤2×105
- ∑n≤2×105sum nle 2 imes 10^5∑n≤2×105
思路
数据范围不允许 O(n2)O(n^2)O(n2) 的解,需要一些小巧思来优化复杂度。
首先找到数组中最大的元素 mxmxmx,与其自己做按位与运算,得到的答案不一定最优,但一定不劣于大多数解法。
很自然地能够想到,定下其中一个元素为 mxmxmx,然后扫描其余所有元素,计算其与 mxmxmx 的按位与结果是否大于 mxmxmx,求出最大答案即可。
时间复杂度 O(n)O(n)O(n)。
Code
#include M
题目大意
有一扇大小为 100×100100 imes 100100×100 的窗户和 nnn 个对角线长为 222 的正方形窗花。以 (0,0)(0,0)(0,0) 为窗户左下角的坐标,右上角的坐标为 (100,100)(100,100)(100,100),第 iii 个窗花的中心在整坐标点 (xi,yi)(x_i,y_i)(xi,yi) 上,窗花的对角线与坐标轴平行。
求出被窗花至少覆盖一次的面积大小。
其中
- 1≤n≤1041le nle 10^41≤n≤104
- 1≤xi,yi≤991le x_i,y_ile 991≤xi,yi≤99
思路
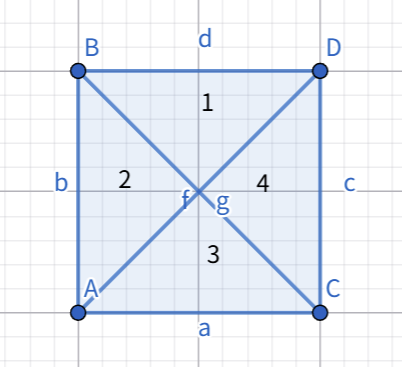
如下图所示,将一个单位正方形分为四个部分,每个部分的面积为 0.250.250.25,以其左下角为基准坐标。
令 f[i][j][k]f[i][j][k]f[i][j][k] 为坐标为 (i,j)(i,j)(i,j) 的第 kkk 部分是否被覆盖至少一次,分类讨论:
- 若中心坐标在图中 AAA 点,那么覆盖的部分是 222 与 333,将 f[i][j][2]f[i][j][2]f[i][j][2] 与 f[i][j][3]f[i][j][3]f[i][j][3] 置为 111。
- 若中心坐标在图中 DDD 点,那么覆盖的部分是 111 与 444,将 f[i][j][1]f[i][j][1]f[i][j][1] 与 f[i][j][4]f[i][j][4]f[i][j][4] 置为 111。
其余情况类似。扫描每个单位正方形的每个部分,若该部分状态为 111,则将答案累加 0.250.250.25。
时间复杂度 O(100×100×4)O(100 imes 100 imes 4)O(100×100×4)。
Code
#include D
题目大意
给定一个整数 nnn。
现在所有包含 xxx 的数字都消失了,找出 nnn 在所有还未消失的自然数中从小到大排在第几位。
输入有 TTT 组测试数据。
其中
- 1≤T≤1051le Tle 10^51≤T≤105
- 0≤n≤10180le nle 10^{18}0≤n≤1018
- 1≤x≤91le xle 91≤x≤9
输入保证 nnn 中不含数字 xxx。
思路
有一个比较玄学的做法。
将 nnn 中所有大于 xxx 的数位减去 111,得到一个新的十进制数 mmm,然后将其转为 999 进制再加上 111 (因为 000 也属于自然数,但进制转换中把它忽略掉了,所以还需要加 111)即为答案。
时间复杂度 O(Tlogn)O(Tlog n)O(Tlogn)。
Code
#include L
题目大意
LNC 喜欢所有 kkk 进制下所有数位的乘积为自身因子的数。他称之为 LNC 数。例如:
当 k=10k = 10k=10 时,y=(36)10y = (36)_{10}y=(36)10 是 LNC 数,因为 (3×6)∣36(3 imes 6) mid 36(3×6)∣36。
当 k=4k = 4k=4 时,y=(12)4y = (12)_4y=(12)4 是 LNC 数,因为转换成十进制后 (12)4=(6)10(12)_4 = (6)_{10}(12)4=(6)10,而 (1×2)∣6(1 imes 2) mid 6(1×2)∣6。
当 k=2k = 2k=2 时,y=(1101)2y = (1101)_2y=(1101)2 不是 LNC 数,因为转换成十进制后 (1101)2=(13)10(1101)_2 = (13)_{10}(1101)2=(13)10,而 000 不是 131313 的因子。
LNC 在和 LJJ 玩一个游戏,LJJ 给出 xxx 枚棋子,然后 LNC 选定一个整数 kkk (k≥2k geq 2k≥2)。随后他们交替取走若干枚棋子,要求取走的棋子数量是 kkk 进制意义下的 LNC 数。LNC 先手,先取完的获胜。两个人都绝顶聪明,故都会选择最优的策略。
LJJ 觉得这个游戏很不公平,他们一共玩了 TTT 局游戏,对于每局游戏他给出的 xxx,他希望知道最小的 kkk 使得 LNC 先手必胜。
其中:
思路
先考虑简单情况。二进制内的LNC数有 111,三进制内的LNC数有 111 和 222。
在 kkk 为 222 时,剩余棋数为奇数时显然必胜,偶数时必败。
kkk 为 333 时,如果剩余棋数是 333 的倍数,那么这个局面先手必败(先手取 111 或者取 222,后手将剩余棋数模 333 后剩余的部分拿掉就行)。
推广到任意情况,对于任意 kkk,如果剩余棋数是它的倍数,那么先手必败。
如果均选择最优策略,那么一回合下来,会拿走 kkk 个棋子。若经过若干回合后剩下的棋子数必会小于 kkk,先手拿走剩下的所有棋子赢下比赛。
也就是说,x%k≠0x % k eq 0x%k=0 时,先手必胜。
暴力枚举 kkk,找到第一个满足 x%k≠0x % k eq 0x%k=0 的 kkk 即可。
Code
#include C
题目大意
Shirost 作为树王国的庆典设计师,准备邀请 nnn 个嘉宾来参加本次庆典。庆典上一共准备了 2n2n2n 个座位,一个座位最多只能坐一个人且一个人恰好坐一个座位。Shirost 初步计划将第 iii 个嘉宾安排在第 iii 个座位上。但是总统调查了这 nnn 个嘉宾的意愿,第 iii 个嘉宾的心仪座位为第 aia_iai 个座位。但除非能坐到心仪座位上,否则他们只愿意坐在原来的座位上。总统希望 Shirost 能够修改计划,使得尽可能多的嘉宾坐在他们的心仪座位上。
给定一个长为 nnn 的数组 {a}{a}{a},找到长为 nnn 的数组 bi (1≤i≤n,1≤bi≤2×105)b_i (1le ile n,1le b_ile 2 imes 10^5)bi (1≤i≤n,1≤bi≤2×105),满足 ∀i≠j,bi≠bj orall i eq j,b_i eq b_j∀i=j,bi=bj 且 ∀i,bi=i orall i,b_i=i∀i,bi=i 或 bi=aib_i=a_ibi=ai,最大化 bi=aib_i=a_ibi=ai 的个数。
其中
- 1≤n≤1051le nle 10^51≤n≤105
- 1≤ai≤2n1le a_ile 2n1≤ai≤2n
思路
对于每个 a[i]a[i]a[i],表示坐在第 iii 号座位的嘉宾希望坐在座位 a[i]a[i]a[i]上。建立有向边 (i,a[i])(i, a[i])(i,a[i]),表示第 iii 位嘉宾希望移动至 a[i]a[i]a[i]。
因为每个点的出度一定不大于 111,所以不可能存在两个环共用一条路径的情况,那么形成的图集一定是由若干 DAGDAGDAG 和若干只含有一个环的有向图组成。
DAGDAGDAG 很好理解,如果其中出度为 000 的点大于 nnn,就找以其为终点的最长路径,这张图对答案的贡献就是最长的路径长度。如果小于等于 nnn,那么这张图就移不动了,对答案的贡献为 000。
如果这张图存在环,那么对答案的贡献就是环大小。
可以使用拓扑排序加工出所有环大小之和,然后再在所有终点编号大于 nnn 的所有 DAGDAGDAG 上跑一遍 DPDPDP 以求出最大路径长,然后将所有求出来的东西取加和,则为最后的答案。
至于如何找出所有 DAGDAGDAG 上节点对应的终点,建反图后以终点为起点跑一遍 dfsdfsdfs 就行了。
时间复杂度 O(n)O(n)O(n)。
Code
#include B
题目大意
一个 n×mn imes mn×m 的字符矩阵 aija_{ij}aij,被称为合法的表达式矩阵,当且仅当其满足如下条件:
- 矩阵只包含 ‘1’,‘+’,‘*’ 字符。
- 对于矩阵的每行从左向右组成的字符串,均为合法的表达式。
- 对于矩阵的每列从上向下组成的字符串,均为合法的表达式。
一个合法的表达式矩阵的权值定义为,每行从左向右组成的字符串和每列从上向下组成的字符串共 n+mn + mn+m 个表达式求值后的值求和的结果。
求所有 n×mn imes mn×m 的合法表达式矩阵中,权值最小的那一个。如果有多个最小的答案,你可以给出任意一个。
我们定义字符串 sss 是合法表达式如下:
- 如果 s=111…111⏞至少一个 1s = overbrace{111dots111}^{ ext{至少一个 }1}s=111…111至少一个 1,则 sss 是合法表达式。
- 如果 sss 和 ttt 均为合法表达式,则 sss * ttt 也是合法表达式。
- 如果 sss 和 ttt 均为合法表达式,则 sss + ttt 也是合法表达式。
其中
- 3≤n,m≤93le n,mle 93≤n,m≤9
思路
有一个很直观的想法就是,将外围全部填上 111(为了保证所有行列表达式合法),然后在内部交替填上 ∗*∗ 和 111,这样保证能够存在最多的,对权值无贡献的 1∗11*11∗1 结构。
但这样构造显然存在问题。
例如 n=m=5n=m=5n=m=5 的情况构造出的矩阵如下
1 1 1 1 11∗1∗11 1∗1 11∗1∗11 1 1 1 1 1 1 1 1 1 1*1*1 1 1*1 1 1*1*1 1 1 1 1 1 1 1 1 1 11∗1∗11 1∗1 11∗1∗11 1 1 1 1
得出的权值为 446904469044690。
有另一种构造方法如下
1 1 1 1 11∗1∗11 1+1 11∗1∗11 1 1 1 1 1 1 1 1 1 1*1*1 1 1+1 1 1*1*1 1 1 1 1 1 1 1 1 1 11∗1∗11 1+1 11∗1∗11 1 1 1 1
得出的权值为 444924449244492,小于上面的 446904469044690,所以交替填乘号不一定是最优解。
对比两个构造方法,可以发现区别在于 11×1111 imes 1111×11 和 11+1111+1111+11 上,前者结果为 121121121,后者结果为 222222,明显后者对总权值的大小贡献较小。
同时因为 1×11 imes 11×1 优于 1+11+11+1,所以还需要尽量保留 1×11 imes 11×1 的结构。
因为数据范围较小,可以考虑乱搞。
先按照之前的错误方法(外围全填 111 内部交替填乘号)构造出矩阵,然后对上面的所有乘号进行替换,检查替换后的权值是否最小。用 dfsdfsdfs 暴力搜索出所有正确答案后,打表输出即可。
Code
用于打表的程序
#include 用于提交的程序
#include