Simulink学习电力系统应用——基础篇(一)
因学习研究的目的,接触了《Matlab/Simulink电力系统建模与仿真》这本书籍,并写下推文帮助自己学习深化,有兴趣深入学习Simulink在电力系统应用的同学可以自行采购,大家一起共同学习讨论。在正式学习之前,我们得先弄清楚Simulink到底是解决什么问题的。
一、Simulink用途
总的来说,Simulink常被用于求解常微分方程、传递函数和状态方程解。具体而言,在分析电力系统的动态特性时,常微分方程可以描述系统中各种物理量随时间的变化关系;传递函数则能反映系统输入与输出之间的关系,帮助我们了解系统的性能;状态方程解可以让我们清晰地掌握系统在不同时刻的状态。通过Simulink,我们能够更高效、准确地得到这些方程的解,从而为电力系统的设计、分析和优化提供有力支持。
二、基于Simulink的数值计算方法
Simulink在求解上述问题时,采用了多种数值计算方法。基于泰勒级数理论,主要分为欧拉法(Euler)、阿达姆斯法(Ad-ams)、龙格-库塔法(Rung-Kutta)。这些方法各有特点和适用场景,在后续的学习中,我们会根据具体的问题选择合适的方法。了解这些数值计算方法的原理和应用,对于我们深入掌握Simulink在电力系统中的应用是非常关键的一步。它们就像是我们手中的工具,只有熟练掌握,才能在面对各种复杂的电力系统问题时游刃有余。
2.1 欧拉法原理
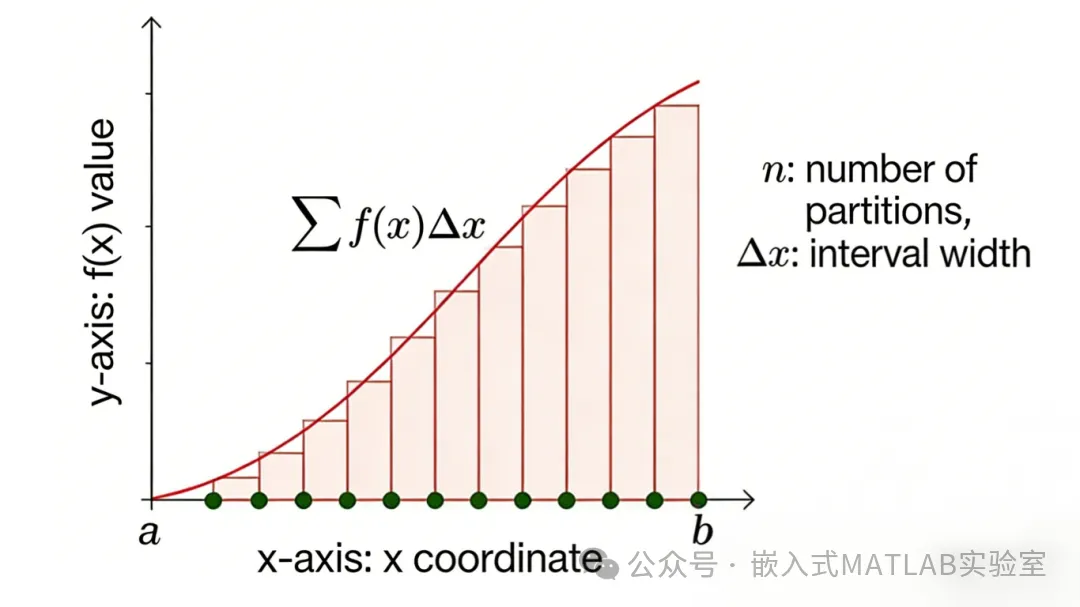
欧拉法(Euler)是一种通过矩形面积近似积分计算的方法。虽然它简单易懂,但精度不高,目前在实际应用中很少使用,其具体原理如下:
假设函数y=f(x),要计算从x=a到x=b这个区间内函数曲线下的面积,把从a到b的这个大区间,划分成许多宽度相等的小区间,每个小区间的宽度记为Δx。(小区间越多,也就是Δx越小,那么我们用矩形面积近似积分的效果就越好。这是因为当小区间足够小时,矩形的形状就更接近函数曲线下的真实形状,近似值也就更接近真实的积分值。
接着,对于每个小区间,我们以小区间的左端点的函数值作为矩形的高度,小区间宽度Δx作为矩形的宽度,这样就构造出了一个个矩形。例如在第i个小区间,左端点是xi,对应的函数值是f(xi),那么这个矩形的面积就是f(xi)Δx。最后,我们把所有这些小矩形的面积加起来,就得到了对积分的近似值。虽然这种方法直观简单,但由于它只是用矩形去近似曲线下的面积,忽略了曲线的弯曲变化,所以在精度要求较高的情况下,就不太适用了。不过,欧拉法作为一种基础的数值计算方法,对于我们理解积分近似计算的基本思想还是很有帮助的。
2.2 阿达姆斯法原理
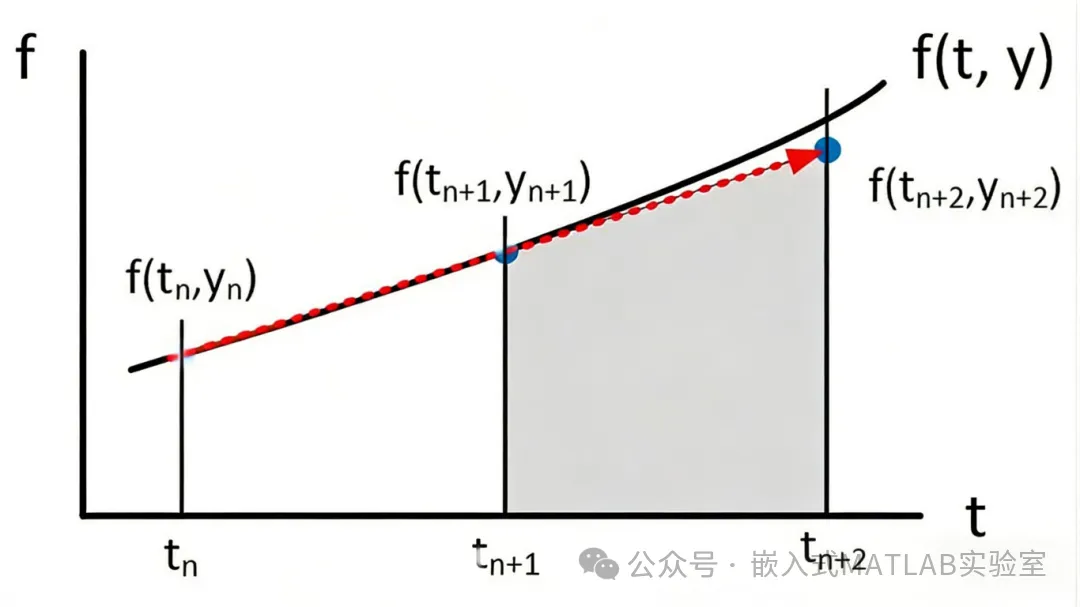
根据插值多项式的节点是否包含待求点tn+1,阿达姆斯法分为显式阿达姆斯-巴什福思法(Adams-Bashforth,AB法)和隐式阿达姆斯-莫尔顿法(Adams-Moulton,AM法)。这二者是阿达姆斯法的基础,它们的性能互补。(显式阿达姆斯-巴什福思法是一种显式的方法,它可以直接根据已知的节点信息计算出下一步的近似值,计算相对简单,但精度可能稍低。而隐式阿达姆斯-莫尔顿法需要通过迭代求解,计算过程相对复杂,但精度较高。在实际应用中,我们可以根据具体的问题和对精度、效率的要求,选择合适的方法。)
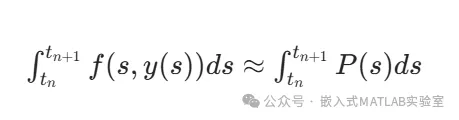
2.3 龙格 - 库塔法原理
龙格-库塔法(Rung-Kutta)通过泰勒级数展开式的方法,在积分区间内多预报几个点的斜率,然后进行加权平均,近似替代微分方程的真实斜率,避免了高阶泰勒展开法中复杂的高阶偏导数计算。对于m阶龙格-库塔法,在区间[tn,tn+1]内取m个采样点,其通用求解公式为:

其中,各斜率ki的计算规则为:

其具体的计算过程分为几个步骤:
1)第一步估算。我们首先计算从当前位置开始,基于当前的斜率,预测下一个位置的变化。这就像是我们根据当前的行驶速度和方向,大致估算下一个时刻的位置。
2)第二步修正。然后我们不止一次估算未来的位置,而是根据第一步的估算,计算一个新的斜率,基于新的斜率再做一次预测。这一步相当于对第一步的估算进行修正,考虑到函数可能的变化。
3)第三步再修正。接着我们再计算出第二步的估算结果的变化,再进行一次调整。
最后,通过综合这些中间估算结果,我们得到一个更精确的未来位置。这个过程实际上就是通过更多的计算步骤来提高预测的准确度,在处理复杂的微分方程问题时,龙格-库塔法具有明显的优势。
三、常微分方程求解算法分类
后续我们求解常微分方程(Ode)数值解时,就是基于上述三类基本方法展开,分为可变步长类算法和固定步长类算法。
可变步长算法就是在结算模型时可以自动调整步长,并通过减少步长来提高计算精度。这种算法的优点是能够根据问题的复杂程度和精度要求,自动调整计算步长。当问题比较复杂,需要更高的精度时,它会自动减小步长,以获得更准确的结果;而当问题相对简单时,它会增大步长,提高计算效率。这样可以在保证计算精度的同时,尽量减少计算量,提高计算的整体效率。
固定步长类算法则是保持步长不变。它在计算过程中,始终使用相同的步长进行计算。这种算法的优点是计算过程相对简单,易于实现。但它的缺点也很明显,由于步长固定,无法根据问题的实际情况进行调整,可能会在某些情况下导致计算精度不足或者计算效率低下。在实际应用中,我们需要根据具体的问题和要求,选择合适的算法。比如对于一些对精度要求不高、计算规模较小的问题,固定步长类算法可能是一个不错的选择;而对于精度要求较高、问题较为复杂的情况,可变步长类算法可能更合适。
四、可变步长与固定步长算法介绍

可变步长类算法中主要有Ode45和Ode23:
1)Ode45基于显式四/五阶Rung-Kutta算法,属于单步解法,计算出当前的解,不需要附加初始值。它在处理一般的常微分方程问题时表现良好,能够在保证一定精度的前提下,高效地计算出结果。
2)Ode23基于显式二/三阶Rung-Kutta算法,也属于单步解法,在计算略带刚性问题上有优势。(刚性问题是指对于一个常微分方程组,其雅可比矩阵的特征值相差悬殊,其方程组可以称为刚性方程组)为了保持解法的稳定性,步长选取存在困难。Ode23能够在处理这类刚性问题时,通过合理调整步长,保证计算的稳定性和精度。
固定步长类算法中主要有Ode5和Ode4。
1)Ode5是固定步长的Ode45算法,它继承了Ode45的一些优点,同时由于步长固定,计算过程更加简单。
2)Ode4是四阶的龙格-库塔法,它在计算精度和效率之间取得了一定的平衡。
在实际应用中,我们可以根据具体的问题特点和要求,选择合适的算法。如果对计算精度要求较高,且问题不是刚性问题,Ode45可能是一个好的选择;如果是刚性问题,Ode23可能更合适;而对于一些对计算效率要求较高、精度要求相对较低的问题,Ode5和Ode4可能是不错的选择。
想要关注更多MATLAB资料的同学,可以微信搜“嵌入式MATLAB实验室”公众号!!